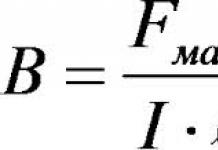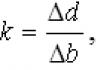Methods for defining a plane on a diagram. Methods for defining a plane in a drawing Methods for defining and properties of numerical planes

5.1 Setting the plane

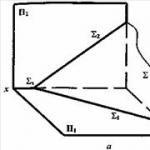
The plane is defined by three arbitrary points that do not belong to the same line. The plane in space can be specified:

· three points that do not lie on the same straight line (Figure 5.1, A);

· a straight line and a point not belonging to it (Figure 5.1, b);

· two intersecting straight lines (Figure 5.1, V);

· two parallel straight lines (Figure 5.1, G);

· any flat figure (Figure 5.1, d).

Figure 5.1

Each of the listed methods for specifying a plane allows transition to any other, because the position of a line in a plane is determined by its two points or one point and the direction of this line.

The method of defining a plane using straight lines (mutually intersecting or parallel) along which this plane intersects with the projection planes P 1 P 2, P 3 is often used. Besides - This is the definition of a plane with traces, while maintaining the clarity of the image (Figure 5.2).

Figure 5.2

5.2 Plane traces.

The line of intersection of the plane under consideration with the projection plane (P 1 , P 2, P 3 ) called the trace of the plane. In other words, the trace of a plane is a straight line lying in the projection plane. The trace is assigned the name of the projection plane to which it belongs. For example, a horizontal trace is obtained when a given plane intersects with plane P 1 and is designated , frontal - with plane P 2 (), profile - with plane P 3 (). Two traces of the same plane intersect on the projection axis at a point called the vanishing point of the traces. Each of the traces of the plane coincides with its projection of the same name, the remaining projections turn out to lie on the axes. For example, the horizontal trace of the plane Σ (Figure 5.2) coincides with its horizontal projection, its frontal projection is on the axis X, and the profile on the axis u. By the location of the traces of the plane, one can judge the position of this plane in space relative to the projection planes P 1, P 2, P 3.

5.3 Position of the plane relative to the projection planes

Any plane arbitrarily taken in space can occupy a general or particular position. A general plane is a plane that is not perpendicular to any of the projection planes (see Figure 5.2). All other planes (except for projection planes) belong to the planes of particular position and are divided into projecting planes and level planes. |A projecting plane is a plane perpendicular to one
from projection planes. For example, the horizontal projection plane is perpendicular to the horizontal projection plane P 1 (Figure 5.3).

Figure 5.3

Horizontal projections of all geometric images (points, lines, figures) lying in this plane coincide with the horizontal trace 1. The angle that is formed between the planes and P 2 is projected onto P 1 without distortion. Frontal trace 2 is perpendicular to the x-axis.

The frontal projection plane () is perpendicular to the frontal plane P 2 is shown in Figure 5.4. Frontal projections of all geometric images (points, lines, figures) lying in this plane coincide with the frontal trace of plane 2. The angle that is formed between the given plane and P 1 is projected onto P 2 without distortion. The horizontal trace of plane 1 is perpendicular to the x-axis.

Figure 5.4

The profile-projecting plane T (T 1, T 2) is perpendicular to the profile projection plane P 3 (Figure 5.5).

Figure 5.5

Profile projections of all geometric images (points, lines, figures) lying in this plane coincide with the profile trace of the T 3 plane . Angles and that are formed between a given plane and the planes of projections P 1 and P 2 (= T^P 1 ; = T^P 2 ), projected onto the P 3 plane without distortion. Horizontal and frontal traces of the plane are parallel to the axis X.

The profile-projecting plane can pass through the x-axis: (Figure 5.6).

Figure 5.6

The traces of this 1 = 2 plane coincide with each other and with the x-axis, so they do not determine the position of the plane. In addition to the traces, it is necessary to specify a point in the plane (Figure 5.6). In a particular case, this plane can be a bisector plane. Angle ° = °, and point A is equidistant from the projection planes P 1 and P 2 . A level plane is a plane that is simultaneously perpendicular to two projection planes and parallel to a third. There are three types of such planes (Figure 5.7):

· the horizontal plane of the level is perpendicular to P 2, P 3 and parallel to P 1 (Figure 5.7, A);

· the frontal plane of the level is perpendicular to P 1, P 3 and parallel to P 2 (Figure 5.7, b);

· the profile plane of the level is perpendicular to P 1, P 2 and parallel to P 3 (Figure 5.7 V).

Figure 5.7

From the definition of level planes it follows that one of the projections of a point, line, figure belonging to these planes will coincide with the trace of the level plane of the same name, and the other projection will be the natural size of these geometric images.

5.4 Signs of belonging to a point and a straight plane

To determine whether a point belongs to a straight plane located in space, one should be guided by the following provisions:

· a point belongs to a plane if a line lying in the plane can be drawn through it;

· a straight line belongs to a plane if it has at least two common points with the plane;

· a straight line belongs to a plane if it passes through a point of a given plane parallel to a straight line belonging to this plane.

An infinite number of lines can be drawn through one point on a plane. These can be arbitrary lines and lines that occupy a special position in relation to the projection planes P 1 P 2, P 3 . A straight line belonging to the plane under consideration, drawn parallel to the horizontal plane of projections, is called r horizontally plane.

A straight line belonging to the plane under consideration, drawn parallel to the frontal plane of projections, is called frontal plane.

The horizontal and front lines are level lines.

The horizontal plane should begin to be constructed from the frontal projection, because it is parallel to the axis x, the horizontal projection of the horizontal is parallel to the horizontal trace of the plane.

And since all the horizontals of the plane are parallel to each other, we can consider the horizontal trace of the plane to be the zero horizontal (Figure 5.8).

The front of the plane should begin to be constructed from a horizontal projection, because it is parallel to the x-axis, the frontal projection of the frontal is parallel to the frontal trace. The frontal trace of the plane is zero frontal. All fronts of the plane are parallel to each other (Figure 5.9).

Figure 5.8

Figure 5.9

The level line also includes a profile straight line lying in a given plane and parallel to P 3 .

The main lines of special position in the plane, in addition to the level line, include the lines of the greatest inclination of the plane to the projection plane.

5.5 Determining the angle of inclination of the plane to the projection planes

A general plane, located arbitrarily in space, is inclined to the projection planes. To determine the magnitude of the dihedral angle of inclination of a given plane to any projection plane, the lines of the greatest inclination of the plane to the projection plane are used: to P 1 - the slope line, to P 2 - the line of the greatest inclination of the plane to the plane P 2.

The lines of greatest inclination of the plane are straight lines that form the greatest angle with the projection plane and are drawn in the plane perpendicular to the corresponding level line. The line of greatest inclination and its corresponding projection form a linear angle, which measures the value of the dihedral angle formed by this plane and the plane of projections (Figure 5.10).

The position of a plane in space is determined by its three points that do not lie on the same straight line. Therefore, to define a plane on a diagram, it is enough to specify three of its points (Fig. 206). The plane can be defined by a point and a straight line (Fig. 207, a), two parallel straight lines (Fig. 207, b), two intersecting straight lines (Fig. 207, c), a triangle (Fig. 207, d).

You can define a plane with traces. The trace of a plane is the straight line along which this plane intersects the projection plane. In Fig. 208 Pv - frontal trace of plane P, Рн - horizontal trace of plane P, Pw - profile trace of plane P.

Various cases of arrangement of planes relative to projection planes

General plane - a plane located obliquely to all projection planes (Fig. 208). Such a plane intersects with three projection planes along straight lines, which are traces of this plane. Each pair of traces converges at a point called the vanishing point of the plane traces and is located on the projection axis. A general position plane has three vanishing points, which are designated Px, Py, Pz. At these points the plane intersects the coordinate axes. Plane figures lying in a general plane are projected with distortion.

Projection plane - a plane perpendicular to any projection plane.

Horizontal projection plane - plane perpendicular to the horizontal plane of projections H (Fig. 209).

Frontal projection plane - plane perpendicular to the frontal plane of projection (Fig. 210).

Profile-projecting plane - plane perpendicular to the profile plane of projections (Fig. 211).

The projecting plane is projected onto the projection plane to which it is perpendicular to a straight line. Pa fig. 209 plane P is horizontally projecting, ΔАВС, lying in the plane P, is projected into a straight line segment that coincides with the trace of the plane Рн. In Fig. 210 ΔDEF, belonging to the frontally projecting plane R, is projected into a segment coinciding with the trace of the plane Rv. In Fig. 211 ΔKMN, lying in the profile-projecting plane Q, is projected onto the W plane into a segment coinciding with the trace of the Qw plane. Therefore, projection planes are often used as auxiliary planes in various constructions. For example, in order to draw a horizontally projecting plane through straight AB (Fig. 212), it is enough to draw a horizontal trace of this plane through the horizontal projection of straight AB, since everything that lies in this plane, including straight AB, is projected onto its horizontal track. The frontal trace of the frontally projecting plane coincides with the frontal projection of straight line a"b" (Fig. 213). The traces of the projecting planes on other projection planes are perpendicular to the corresponding projection axes (see Fig. 209, 210, 211).

Rice. 212 Fig. 213

Planes perpendicular to two projection planes are parallel to the third projection plane . Geometric figures lying in these planes are projected without distortion onto the projection plane to which this plane is parallel (Fig. 214, 215; 216). Such planes are called the same as the projection plane parallel to which they are located: horizontal plane (Fig. 214), frontal plane (Fig. 215), profile plane (Fig. 216).

In planimetry, the plane is one of the main figures, therefore, it is very important to have a clear understanding of it. This article was created to cover this topic. First, the concept of a plane, its graphical representation is given and the designations of planes are shown. Next, the plane is considered together with a point, a straight line or another plane, and options arise from their relative positions in space. In the second and third and fourth paragraphs of the article, all the options for the relative position of two planes, a straight line and a plane, as well as points and planes are analyzed, the basic axioms and graphic illustrations are given. In conclusion, the main methods of defining a plane in space are given.

Page navigation.

Plane - basic concepts, symbols and images.

The simplest and most basic geometric figures in three-dimensional space are a point, a straight line and a plane. We already have an idea of a point and a line on a plane. If we place a plane on which points and lines are depicted in three-dimensional space, then we get points and lines in space. The idea of a plane in space allows us to obtain, for example, the surface of a table or wall. However, a table or wall has finite dimensions, and the plane extends beyond its boundaries to infinity.

Points and lines in space are designated in the same way as on a plane - in large and small Latin letters, respectively. For example, points A and Q, lines a and d. If two points lying on a line are given, then the line can be denoted by two letters corresponding to these points. For example, straight line AB or BA passes through points A and B. Planes are usually denoted by small Greek letters, for example, planes, or.

When solving problems, it becomes necessary to depict planes in a drawing. A plane is usually depicted as a parallelogram or an arbitrary simple closed region.

A plane is usually considered together with points, straight lines or other planes, and various options for their relative positions arise. Let's move on to their description.

The relative position of the plane and the point.

Let's start with the axiom: there are points in every plane. From it follows the first option for the relative position of the plane and the point - the point can belong to the plane. In other words, a plane can pass through a point. To indicate that a point belongs to a plane, the symbol “” is used. For example, if the plane passes through point A, then you can briefly write .

It should be understood that on a given plane in space there are infinitely many points.

The following axiom shows how many points in space must be marked so that they define a specific plane: through three points that do not lie on the same line, a plane passes, and only one. If three points lying in a plane are known, then the plane can be denoted by three letters corresponding to these points. For example, if a plane passes through points A, B and C, then it can be designated ABC.

Let us formulate another axiom, which gives the second version of the relative position of the plane and the point: there are at least four points that do not lie in the same plane. So, a point in space may not belong to the plane. Indeed, by virtue of the previous axiom, a plane passes through three points in space, and the fourth point may or may not lie on this plane. When writing briefly, use the symbol “”, which is equivalent to the phrase “does not belong”.

For example, if point A does not lie in the plane, then use a short notation.

Straight line and plane in space.

Firstly, a straight line can lie in a plane. In this case, at least two points of this line lie in the plane. This is established by the axiom: if two points of a line lie in a plane, then all points of this line lie in the plane. To briefly record the belonging of a certain line to a given plane, use the symbol “”. For example, the notation means that straight line a lies in the plane.

Secondly, a straight line can intersect a plane. In this case, the straight line and the plane have one single common point, which is called the point of intersection of the straight line and the plane. When writing briefly, I denote the intersection with the symbol “”. For example, the notation means that straight line a intersects the plane at point M. When a plane intersects a certain straight line, the concept of an angle between the straight line and the plane arises.

Separately, it is worth focusing on a straight line that intersects the plane and is perpendicular to any straight line lying in this plane. Such a line is called perpendicular to the plane. To briefly record perpendicularity, use the symbol “”. For a more in-depth study of the material, you can refer to the article perpendicularity of a straight line and a plane.

Of particular importance when solving problems related to the plane is the so-called normal vector of the plane. A normal vector of a plane is any non-zero vector lying on a line perpendicular to this plane.

Thirdly, a straight line may be parallel to the plane, that is, it may not have common points in it. When writing concurrency briefly, use the symbol “”. For example, if line a is parallel to the plane, then we can write . We recommend that you study this case in more detail by referring to the article parallelism of a line and a plane.

It should be said that a straight line lying in a plane divides this plane into two half-planes. The straight line in this case is called the boundary of the half-planes. Any two points of the same half-plane lie on the same side of a line, and two points of different half-planes lie on opposite sides of the boundary line.

Mutual arrangement of planes.

Two planes in space can coincide. In this case they have at least three points in common.

Two planes in space can intersect. The intersection of two planes is a straight line, which is established by the axiom: if two planes have a common point, then they have a common straight line on which all the common points of these planes lie.

In this case, the concept of an angle between intersecting planes arises. Of particular interest is the case when the angle between the planes is ninety degrees. Such planes are called perpendicular. We talked about them in the article perpendicularity of planes.

Finally, two planes in space can be parallel, that is, have no common points. We recommend that you read the article parallelism of planes to get a complete understanding of this option for the relative arrangement of planes.

Methods for defining a plane.

Now we will list the main ways to define a specific plane in space.

Firstly, a plane can be defined by fixing three points in space that do not lie on the same straight line. This method is based on the axiom: through any three points that do not lie on the same line, there is a single plane.

If a plane is fixed and specified in three-dimensional space by indicating the coordinates of its three different points that do not lie on the same straight line, then we can write the equation of the plane passing through the three given points.

The next two methods of defining a plane are a consequence of the previous one. They are based on corollaries of the axiom about a plane passing through three points:

a plane passes through a line and a point not lying on it, and only one (see also the article equation of a plane passing through a line and a point);
There is only one plane passing through two intersecting lines (we recommend that you read the material in the article: equation of a plane passing through two intersecting lines).

The fourth way to define a plane in space is based on defining parallel lines. Recall that two lines in space are called parallel if they lie in the same plane and do not intersect. Thus, by indicating two parallel lines in space, we will determine the only plane in which these lines lie.

If a plane is given in the indicated way in three-dimensional space relative to a rectangular coordinate system, then we can create an equation for a plane passing through two parallel lines.

In high school geometry lessons, the following theorem is proven: through a fixed point in space there passes a single plane perpendicular to a given line. Thus, we can define a plane if we specify the point through which it passes and a line perpendicular to it.

If a rectangular coordinate system is fixed in three-dimensional space and a plane is specified in the indicated way, then it is possible to construct an equation for a plane passing through a given point perpendicular to a given straight line.

Instead of a line perpendicular to the plane, you can specify one of the normal vectors of this plane. In this case, it is possible to write

Introduction

From the planimetry course we know that a plane is a set whose elements are points and in which the system of planimetry axioms is satisfied, describing the properties of points and straight lines.

Space is a set whose elements are points and in which the system of axioms of stereometry is fulfilled, describing the properties of points, lines and planes. The system of axioms of stereometry gives a description of the properties of space and its main elements. The concepts of “point”, “straight line” and “plane” are accepted without definitions: their description and properties are contained in the axioms. On the other hand, the concepts of “point”, “straight”, “plane” have a clear meaning, reflected in the drawings and drawings.

The study of space leads to the need to expand the system of planimetry axioms and consider a new group of axioms that express the properties of the relative positions of points, straight lines and planes, which is especially important for us in space.

The purpose of the abstract is to get a clear idea of space and the ways of arranging planes in space.

To achieve this goal, the following tasks are set:

- consider ways to define planes in space,
- consider the basic axioms of stereometry;
- study possible options for the relative arrangement of planes in space,
- formulate the main features and properties of the relative arrangement of planes in space;

Methods for defining a plane

The study of space leads to the need to expand the system of axioms.

Let's consider axiom R1. There are planes in space. In each plane of space, all axioms of planimetry are satisfied. This axiom gives us the right to consider in any plane of space segments, straight lines with all their properties that were studied in planimetry. For example, if straight line a and a point M that does not belong to it lie in some plane b, then in this plane it is possible to draw through point M a straight line parallel to line a, and, moreover, only one.

Axiom R3 says: whatever the plane, there are points that belong to this plane and points that do not belong to it. This axiom states that for any plane in space, you can choose any number of points in this plane, as well as any number of points outside it. If point A lies in (belongs to) plane b, then write: A b and say that plane b passes through point A. If point A does not belong to plane b, then write: A b and say that the plane b does not pass through point A.

A plane in space is uniquely determined:

Three points that do not lie on a straight line. Axiom R2 (plane axiom) says: Through any three points that do not belong to the same line, a plane can be drawn, and only one. A plane that passes through points A, B and C that do not belong to the same line (C AB) is designated symbolically (ABC); if this plane is plane b, then write b = (ABC) or (ABC) = b. A table with three legs cannot swing on a flat floor. Its stability is explained by the fact that the ends of its three legs (three points) belong to one plane - the plane of the floor, but do not belong to one straight line. A poorly made table with four legs swings on the flat floor, and they try to put something under one of its legs.

A straight line and a point not lying on a straight line.

According to Theorem 1, through any straight line and a point not belonging to it, one can draw a plane, and only one.

Theorem 2. Through any two intersecting lines you can draw a plane, and only one.

If a straight line passes through two points of a plane, then it lies in this plane

Theorem 3. A unique plane can be drawn through two parallel lines.

Here, from the axioms of stereometry we have accepted, we will obtain important theorems and corollaries about straight lines and planes. By themselves they are quite obvious. Let us consider their proofs, which show how any statement can be strictly deduced from the axioms with all the necessary references.

2.1 Defining a straight line with two points

Proof. In paragraph 1.1 it has already been proven that through every two points A, B there passes a straight line a.

Let us prove that there is only one line. The straight line a lies in a certain plane a. Let us assume that, in addition to straight line a, straight line b also passes through points A and B (Fig. 31). According to Axiom 3, a straight line that has two common points with a plane lies in this plane. Since straight line b has points A and B in common with a, then b lies in the α plane.

Rice. 31

But in plane a, planimetry is performed, and, therefore, only one straight line passes through two points A and B. This means that lines a and b coincide. Thus, only one straight line passes through points A and B.

Consequence. In space (as well as on the plane), two different lines cannot have more than one common point.

Two lines that have a single common point are called intersecting.

Comment. A proposition that is valid in planimetry is not always true in stereometry. So, for example, in a plane through two given points N, S there passes only one circle with a diameter NS, and in the space of such circles there is an infinite number - in each plane passing through the points N, S there lies such a circle (Fig. 32, a) .

Rice. 32

But there is only one straight line passing through points N, S in space. This is the common straight line of all planes passing through points N, S (Fig. 32, b).

Having proved that there is a single straight line passing through every two points in space, we can define a straight line in space by any pair of its points, without worrying about the plane in which this straight line lies. The straight line passing through points A, B is designated (AB).

The same is true for segments: every two points in space serve as the ends of a single segment.

2.2 Defining a plane with three points

Proof. Let points A, B, C do not lie on the same straight line. According to the plane axiom, a certain plane a passes through these points (see Fig. 6). Let's prove that there is only one.

Let us assume that another plane (3, different from a) passes through points A, B, C. Planes a and p have common points (for example, point A). According to axiom 2, the intersection of planes α and β is their common straight line. On this all common points of the planes α and β lie on a straight line, and therefore points A, B, C. But this contradicts the condition of the theorem, since according to it A, B, C do not lie on the same straight line. So, through points A, B, C only one plane α passes through.

A plane passing through three points A, B, C that do not lie on the same straight line is designated (ABC).

It is easy to illustrate Theorem 2. For example, the position of a door is fixed by two door hinges and a lock.

2.3 Specifying a plane with a straight line and a point and two straight lines

Proof. Let a line a and a point A not lying on it be given. Let us take two points B and C on line a (Fig. 33). Point A does not lie on the same straight line with them, since only one straight line passes through points B and C - this is straight line a, and point A does not lie on it according to the conditions of the theorem.

Rice. 33

Through points A, B, C, which do not lie on the same straight line, there passes (by Theorem 2) a single plane ABC. Line a has two common points B and C with it and, therefore, according to axiom 3, lies in it. Thus, plane ABC is the plane passing through line a and point A.

We will prove the uniqueness of such a plane by contradiction.

Let there be another plane β containing line a and point A. Then it contains points B and C. According to Theorem 2, it must coincide with plane ABC. The resulting contradiction proves uniqueness.

Here is an illustration of this theorem: when turning the binding of a book, you fix its position with your fingers at every moment.

Proof. Let lines a and b intersect at point A. Take another point B on line b (Fig. 34). According to Theorem 3, plane a passes through line a and point B. According to axiom 3, straight line b lies in this plane, since it has two common points A and B with it. This means that plane a passes through straight lines a and b. Prove the uniqueness of such a plane yourself by contradiction.