5.1 Задание плоскости

Плоскость задается тремя произвольными точками, не принадле­жащими одной прямой. Плоскость в пространстве можно задать:

· тремя точками, не лежащими на одной прямой (рисунок 5.1, а);

· прямой и не принадлежащей ей точкой (рисунок 5.1, б );

· двумя пересекающимися прямыми (рисунок 5.1, в );

· двумя параллельными прямыми (рисунок 5.1, г );

· любой плоской фигурой (рисунок 5.1, д ).

Рисунок 5.1

Каждый из перечисленных способов задания плоскости допускает переход к любому другому, т.к. положение прямой в плоскости опре­деляется двумя ее точками или одной точкой и направлением этой прямой.

Часто применяется способ задания плоскости с помощью прямых линий (взаимно пересекающихся или параллельных), по которым данная плоскость пересекается с плоскостями проекций П 1 П 2 , П 3 . Кроме этого- это задание плоскости следами, при этом сохраняется наглядность изображения (рисунок 5.2).

Рисунок 5.2

5.2 Следы плоскости.

Линия пересечения рассматриваемой плоскости с плоскостью проекций (П 1 , П 2 , П 3 ) называется следом плоскости. Иными словами, след плоскости - это прямая, лежащая в плоскости проекций. Следу присваивается наименование той плоскости проекций, которой он принадлежит. Например, горизонтальный след получен при пересече­нии заданной плоскости с плоскостью П 1 и обозначается , фрон­тальный - с плоскостью П 2 (), профильный - с плоскостью П 3 (). Два следа одной и той же плоскости пересекаются на оси про­екции в точке, называемой точкой схода следов. Каждый из следов плоскости совпадает со своей одноименной проекцией, остальные проекции оказываются лежащими на осях. Например, горизонтальный след плоскости Σ(рисунок 5.2) совпадает со своей горизонтальной проек­цией , фронтальная его проекция находится на оси х , а профильная на оси у. По расположению следов плоскости можно судить о по­ложении данной плоскости в пространстве относительно плоскостей проекций П 1 ,П 2 , П 3 .

5.3 Положение плоскости относительно плоскостей проекций

Любая, произвольно взятая в пространстве плоскость, может за­нимать общее или частное положение. Плоскостью общего положения называется плоскость, которая не перпендикулярна ни к одной из плоскостей проекций (см. рисунок 5.2). Все остальные плоскости (кроме плоскостей проекций) относятся к плоскостям частного положения и подразделяются на проецирующие плоскости и плоскости уровня. |Проецирующей называется плоскость, перпендикулярная к одной
из плоскостей проекций. Например, горизонтально-проецирующая плоскостьперпендикулярна к горизонтальной плоскости проекции П 1 (рисунок 5.3).

Рисунок 5.3

Горизонтальные проекции всех геометрических образов (точек, прямых, фигур), лежащих в этой плоскости, совпадают с горизон­тальным следом 1 . Угол, который образуется между плоскостями и П 2 , проецируется на П 1 без искажения. Фронтальный след 2 пер­пендикулярен к оси x.

Фронтально-проецирующая плоскость () перпендикулярна к фронтальной плоскости П 2 показана на рисунке 5.4. Фронтальные проекции всех геометрических образов (точек, пря­мых, фигур), лежащих в этой плоскости, совпадают с фронтальным следом плоскости 2 . Угол , который образуется между заданной плоскостью и П 1 , проецируется на П 2 без искажения. Горизонталь­ный след плоскости 1 перпендикулярен к оси x.

Рисунок 5.4

Профильно-проецирующая плоскость Т (T 1 , T 2) перпендикулярна к профильной плоскости проекции П 3 (рисунок 5.5).

Рисунок 5.5

Профильные проекции всех геометрических образов (точек, прямых, фигур), лежащих в этой плоскости, совпадают с профильным следом плоскости Т 3 . Углы и , которые образуются между задан­ной плоскостью и плоскостями проекций П 1 и П 2 (= T^П 1 ; = Т^П 2 ), проецируются на плоскость П 3 без искажений. Горизон­тальный и фронтальный следы плоскости параллельны оси х.

Профильно-проецирующая плоскость может проходить через ось x: (рисунок 5.6).

Рисунок 5.6

Следы этой плоскости 1 = 2 совпадают друг с другом и с осью x, поэтому не определяют положение плоскости. Необходимо кроме следов задать в плоскости точку (рисунок 5.6). В частном случае эта плос­кость может быть биссекторной плоскостью. Угол ° = °, а точка А равноудалена от плоскостей проекций П 1 и П 2 . Плоскостью уровня называется плоскость, перпендикулярная од­новременно к двум плоскостям проекций и параллельная третьей. Та­ких плоскостей три разновидности (рисунок 5.7):

· горизонтальная плоскость уровня перпендикулярна к П 2 , П 3 и параллельна П 1 (рисунок 5.7, а);

· фронтальная плоскость уровня перпендикулярна к П 1 ,П 3 и па­раллельна П 2 (рисунок 5.7, б);

· профильная плоскость уровня перпендикулярна к П 1 , П 2 и параллельна П 3 (рисунок 5.7 в ).

Рисунок 5.7

Из определения плоскостей уровня следует, что одна из проекций точки, линии, фигуры, принадлежащих этим плоскостям, будет совпадать с одноименным следом плоскости уровня, а другая проекция будет натуральной величиной этих геометрических образов.

5.4 Признаки принадлежности точки и прямой плоскости

Для определения принадлежности точки и прямой плоскости, расположенной в пространстве, следует руководствоваться следующими положениями:

· точка принадлежит плоскости, если через нее можно провести линию, лежащую в плоскости;

· прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки;

· прямая принадлежит плоскости, если она проходит через точку данной плоскости параллельно прямой, принадлежащей этой плоскости.

Через одну точку на плоскости можно провести бесконечное мно­жество линий. Это могут быть произвольные линии и линии, зани­мающие особое положение по отношению к плоскостям проекций П 1 П 2 , П 3 . Прямая, принадлежащая рассматриваемой плоскости, прове­денная параллельно горизонтальной плоскости проекций, называется горизонталью плоскости.

Прямая, принадлежащая рассматриваемой плоскости, проведенная параллельно фронтальной плоскости проекций, называется фронталью плоскости.

Горизонталь и фронталь являются линиями уровня.

Горизонталь плоскости следует начинать строить с фронтальной проекции, т.к. она параллельна оси x , горизонтальная проекция гори­зонтали параллельна горизонтальному следу плоскости.

А так как все горизонтали плоскости параллельны между собой, можно считать горизонтальный след плоскости нулевой горизонталью (рисунок 5.8).

Фронталь плоскости следует начинать строить с горизонтальной проекции, т.к. она параллельна оси x, фронтальная проекция фронтали параллельна фронтальному следу. Фронтальный след плоскости - нулевая фронталь. Все фронтали плоскости параллельны между собой (рисунок 5.9).

Рисунок 5.8

Рисунок 5.9

К линии уровня относится и профильная прямая, лежащая в за­данной плоскости и параллельная П 3 .

К главным линиям особого положения в плоскости, кроме линии уровня, относятся линии наибольшего наклона плоскости к плоскости проекций.

5.5 Определение угла наклона плоскости к плоскостям проекций

Плоскость общего положения, расположенная в пространстве произвольно, наклонена к плоскостям проекций. Для определения величины двухгранного угла наклона заданной плоскости к какой-либо плоскости проекции используются линии наибольшего наклона плоскости к плоскости проекций: к П 1 - линия ската, к П 2 - линия наибольшего наклона плоскости к плоскости П 2 .

Линии наибольшего наклона плоскости - это прямые, образующие с плоскостью проекций наибольший угол, проводятся в плоскости перпендикулярно к соответствующей линии уровня. Линии наибольшего наклона и ее соответствующая проекция образуют линейный угол, которым измеряется величина двухгранного угла, составленного данной плоскостью и плоскостью проекций (рисунок 5.10).

Положение плоскости в пространстве определяется тремя ее точками, не лежащими на одной прямой. Поэтому чтобы задать на эпюре плоскость, достаточно задать три ее точки (рис. 206). Плоскость можно задать точкой и прямой (рис. 207, а), двумя параллельными прямыми (рис. 207, б), двумя пересекающимися прямыми (рис. 207, в), треугольником (рис. 207, г).

Можно задать плоскость следами. Следом плоскости называют прямую, по которой данная плоскость пересекает плоскость проекций. На рис. 208 Pv - фронтальный след плоскости Р, Рн - горизонтальный след плоскости Р, Pw - профильный след плоскости Р.

Различные случаи расположения плоскостей относительно плоскостей проекций

Плоскость общего положения - плоскость, расположенная наклонно ко всем плоскостям проекций (рис. 208). Такая плоскость пересекается с тремя плоскостями проекций по прямым, которые являются следами этой плоскости. Каждая пара следов сходится в точке, которая называется точкой схода следов плоскости и располагается на оси проекций. Плоскость общего положения имеет три точки схода, которые обозначаются Рх, Ру, Рz. В этих точках плоскость пересекает оси координат. Плоские фигуры, лежащие в плоскости общего положения, проецируются проекций с искажением.

Проецирующая плоскость - плоскость, перпендикулярная какой-либо плоскости проекций.

Горизонтально - проецирующая плоскость - плоскость, перпендикулярная горизонтальной плоскости проекций Н (рис. 209).

Фронтально - проецирующая плоскость - плоскость, перпендикулярная фронтальной плоскости проекции (рис. 210).

Профильно-проецирующая плоскость - плоскость, перпендикулярная профильной плоскости проекций (рис. 211).

Проецирующая плоскость проецируется на плоскость проекций, к которой она перпендикулярна, в прямую. Па рис. 209 плоскость Р горизонтально-проецирующая, ΔАВС, лежащий в плоскости Р, проецируется в отрезок прямой линии, который совпадает со следом плоскости Рн. На рис. 210 ΔDEF, принадлежащий фронтально-проецирующей плоскости R, проецируется в отрезок, совпадающий со следом плоскости Rv. На рис. 211 ΔKMN, лежащий в профильно-проецирующей плоскости Q, проецируется на плоскость W в отрезок, совпадающий со следом плоскости Qw. Поэтому проецирующие плоскости часто используются в качестве вспомогательных при различных построениях. Например, чтобы через прямую AB провести горизонтально-проецирующую плоскость (рис. 212), достаточно через горизонтальную проекцию прямой ab провести горизонтальный след этой плоскости, так как все, что в этой плоскости лежит, в том числе и прямая AB, проецируется на ее горизонтальный след. Фронтальный след фронтально-проецирующей плоскости совпадает с фронтальной проекцией прямой a"b" (рис. 213). Следы проецирующих плоскостей на других плоскостях проекций перпендикулярны соответствующим осям проекций (см. рис. 209, 210, 211).

Рис. 212 Рис. 213

Плоскости, перпендикулярные двум плоскостям проекций, параллельны третьей плоскости проекций . Геометрические фигуры, лежащие в этих плоскостях, проецируются без искажения на ту плоскость проекций, которой параллельна данная плоскость (рис. 214, 215; 216). Называются такие плоскости так же, как и плоскость проекций, параллельно которой они расположены: горизонтальная плоскость (рис. 214), фронтальная плоскость (рис. 215), профильная плоскость (рис. 216).

В планиметрии плоскость является одной из основных фигур, поэтому, очень важно иметь ясное представление о ней. Эта статья создана с целью раскрытия этой темы. Сначала дано понятие плоскости, ее графическое представление и показаны обозначения плоскостей. Далее плоскость рассматривается вместе с точкой, прямой или другой плоскостью, при этом возникают варианты из взаимного расположения в пространстве. Во втором и третьем и четвертом пункте статьи как раз разобраны все варианты взаимного расположения двух плоскостей, прямой и плоскости, а также точки и плоскости, приведены основные аксиомы и графические иллюстрации. В заключении даны основные способы задания плоскости в пространстве.

Навигация по странице.

Плоскость – основные понятия, обозначения и изображение.

Простейшими и основными геометрическими фигурами в трехмерном пространстве являются точка, прямая и плоскость. Мы уже имеем представление о точке и прямой на плоскости . Если поместить плоскость, на которой изображены точки и прямые, в трехмерное пространство, то мы получим точки и прямые в пространстве. Представление о плоскости в пространстве позволяет получить, к примеру, поверхность стола или стены. Однако, стол или стена имеют конечные размеры, а плоскость простирается за их границы в бесконечность.

Точки и прямые в пространстве обозначаются также как и на плоскости – большими и маленькими латинскими буквами соответственно. Например, точки А и Q , прямые а и d . Если заданы две точки, лежащие на прямой, то прямую можно обозначить двумя буквами, соответствующими этим точкам. К примеру, прямая АВ или ВА проходит через точки А и В . Плоскости принято обозначать маленькими греческими буквами, например, плоскости , или .

При решении задач возникает необходимость изображать плоскости на чертеже. Плоскость обычно изображают в виде параллелограмма или произвольной простой замкнутой области.

Плоскость обычно рассматривается вместе с точками, прямыми или другими плоскостями, при этом возникают различные варианты их взаимного расположения. Переходим к их описанию.

Взаимное расположение плоскости и точки.

Начнем с аксиомы: в каждой плоскости имеются точки. Из нее следует первый вариант взаимного расположения плоскости и точки – точка может принадлежать плоскости. Другими словами, плоскость может проходить через точку. Для обозначения принадлежности какой-либо точки какой-либо плоскости используют символ «». Например, если плоскость проходит через точку А , то можно кратко записать .

Следует понимать, что на заданной плоскости в пространстве имеется бесконечно много точек.

Следующая аксиома показывает, сколько точек в пространстве необходимо отметить, чтобы они определяли конкретную плоскость: через три точки, не лежащие на одной прямой, проходит плоскость, причем только одна. Если известны три точки, лежащие в плоскости, то плоскость можно обозначить тремя буквами, соответствующими этим точкам. Например, если плоскость проходит через точки А , В и С , то ее можно обозначить АВС .

Сформулируем еще одну аксиому, которая дает второй вариант взаимного расположения плоскости и точки: имеются по крайней мере четыре точки, не лежащие в одной плоскости. Итак, точка пространства может не принадлежать плоскости. Действительно, в силу предыдущей аксиомы через три точки пространства проходит плоскость, а четвертая точка может как лежать на этой плоскости, так и не лежать. При краткой записи используют символ «», который равносилен фразе «не принадлежит».

К примеру, если точка А не лежит в плоскости , то используют краткую запись .

Прямая и плоскость в пространстве.

Во-первых, прямая может лежать в плоскости. В этом случае, в плоскости лежат хотя бы две точки этой прямой. Это устанавливается аксиомой: если две точки прямой лежат в плоскости, то все точки этой прямой лежат в плоскости. Для краткой записи принадлежности некоторой прямой данной плоскости пользуются символом «». Например, запись означает, что прямая а лежит в плоскости .

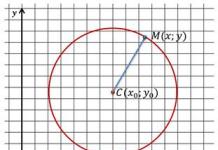
Во-вторых, прямая может пересекать плоскость. При этом прямая и плоскость имеют одну единственную общую точку, которую называют точкой пересечения прямой и плоскости. При краткой записи пересечение обозначаю символом «». К примеру, запись означает, что прямая а пересекает плоскость в точке М . При пересечении плоскости некоторой прямой возникает понятие угла между прямой и плоскостью .

Отдельно стоит остановиться на прямой, которая пересекает плоскость и перпендикулярна любой прямой, лежащей в этой плоскости. Такую прямую называют перпендикулярной к плоскости. Для краткой записи перпендикулярности используют симовл «». Для более глубокого изучения материала можете обратиться к статье перпендикулярность прямой и плоскости .

Особую значимость при решении задач, связанных с плоскостью, имеет так называемый нормальный вектор плоскости . Нормальным вектором плоскости является любой ненулевой вектор, лежащий на прямой, перпендикулярной этой плоскости.

В-третьих, прямая может быть параллельна плоскости, то есть, не иметь в ней общих точек. При краткой записи параллельности используют символ «». Например, если прямая а параллельна плоскости , то можно записать . Рекомендуем подробнее изучить этот случай, обратившись к статье параллельность прямой и плоскости .

Следует сказать, что прямая, лежащая в плоскости, делит эту плоскость на две полуплоскости. Прямая в этом случае называется границей полуплоскостей. Любые две точки одной полуплоскости лежат по одну сторону от прямой, а две точки разных полуплоскостей лежат по разные стороны от граничной прямой.

Взаимное расположение плоскостей.

Две плоскости в пространстве могут совпадать. В этом случае они имеют, по крайней мере, три общие точки.

Две плоскости в пространстве могут пересекаться. Пересечением двух плоскостей является прямая линия, что устанавливается аксиомой: если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

В этом случае возникает понятие угла между пересекающимися плоскостями . Отдельный интерес представляет случай, когда угол между плоскостями равен девяноста градусам. Такие плоскости называют перпендикулярными. О них мы поговорили в статье перпендикулярность плоскостей .

Наконец, две плоскости в пространстве могут быть параллельными, то есть, не иметь общих точек. Рекомендуем ознакомиться со статьей параллельность плоскостей , чтобы получить полное представление об этом варианте взаимного расположения плоскостей.

Способы задания плоскости.

Сейчас мы перечислим основные способы задания конкретной плоскости в пространстве.

Во-первых, плоскость можно задать, зафиксировав три не лежащие на одной прямой точки пространства. Этот способ основан на аксиоме: через любые три точки, не лежащие на одной прямой, проходит единственная плоскость.

Если в трехмерном пространстве зафиксирована и задана плоскость с помощью указания координат трех ее различных точек, не лежащих на одной прямой, то мы можем написать уравнение плоскости, проходящей через три заданные точки .

Два следующих способа задания плоскости являются следствием из предыдущего. Они основаны на следствиях из аксиомы о плоскости, проходящей через три точки:

• через прямую и не лежащую на ней точку проходит плоскость, притом только одна (смотрите также статью уравнение плоскости, проходящей через прямую и точку);
• через две пересекающиеся прямые проходит единственная плоскость (рекомендуем ознакомиться с материалом статьи уравнение плоскости, проходящей через две пересекающиеся прямые).

Четвертый способ задания плоскости в пространстве основан на определении параллельных прямых . Напомним, что две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Таким образом, указав две параллельные прямые в пространстве, мы определим единственную плоскость, в которой эти прямые лежат.

Если в трехмерном пространстве относительно прямоугольной системы координат задана плоскость указанным способом, то мы можем составить уравнение плоскости, проходящей через две параллельные прямые .

В курсе средней школы на уроках геометрии доказывается следующая теорема: через фиксированную точку пространства проходит единственная плоскость, перпендикулярная к данной прямой. Таким образом, мы можем задать плоскость, если укажем точку, через которую она проходит, и прямую, перпендикулярную к ней.

Если в трехмерном пространстве зафиксирована прямоугольная система координат и задана плоскость указанным способом, то можно составить уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой .

Вместо прямой, перпендикулярной к плоскости, можно указать один из нормальных векторов этой плоскости. В этом случае есть возможность написать

Введение

Из курса планиметрии мы знаем, что плоскость - это множество, элементами которого являются точки и в котором выполняется система аксиом планиметрии, описывающая свойства точек и прямы.

Пространство - это множество, элементами которого являются точки и в котором выполняется система аксиом стереометрии, описывающая свойства точек, прямых и плоскостей. Система аксиом стереометрии дает описание свойств пространства и основных его элементов. Понятия «точка», «прямая» и «плоскость» принимаются без определений: их описание и свойства содержатся в аксиомах. С другой стороны, понятия «точка», «прямая», «плоскость» имеют наглядный смысл, отраженный на чертежах и рисунках.

Изучение пространства приводит к необходимости расширить систему аксиом планиметрии и рассмотреть новую группу аксиом, в которых выражены свойства взаимного расположения точек, прямых и плоскостей, что особенно важно для нас, в пространстве.

Цель реферата - получить наглядное представление о пространстве и способах расположения плоскостей в пространстве.

Для выполнения этой цели поставлены следующие задачи:

• - рассмотреть способы задания плоскостей в пространстве,
• - рассмотреть основные аксиомы стереометрии;
• - изучить возможные варианты взаимного расположения плоскостей в пространстве,
• - сформулировать основные признаки и свойства взаимного расположения плоскостей в пространстве;

Способы задания плоскости

Изучение пространства приводит к необходимости расширить систему аксиом.

Рассмотрим аксиому R1. В пространстве существуют плоскости. В каждой плоскости пространства выполняются все аксиомы планиметрии. Эта аксиома дает нам право рассматривать в любой плоскости пространства отрезки, прямые со всеми их свойствами, которые изучались в планиметрии. Например, если прямая а и не принадлежащая ей точка М лежат в некоторой плоскости б, то в этой плоскости можно провести через точку М прямую, параллельную прямой а, и притом только одну.

В аксиоме R3 говорится: какова бы не была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей. Данной аксиомой утверждается, что для любой плоскости в пространстве можно выбрать любое количество точек в этой плоскости, равно как и сколько угодно точек вне её. В случае, если точка А л7+ежит в (принадлежит) плоскости б, то записывают: А б и говорят, что плоскость б проходит через точку А. Если точка А не принадлежит плоскости б, то записывают: А б и говорят, что плоскость б не проходит через точку А.

Плоскость в пространстве однозначно определяется:

Тремя точками, не лежащими на прямой. Аксиома R2 (аксиома плоскости) гласит: Через любые три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну. Плоскость, которая проходит через точки А, В и С, не принадлежащие одной прямой (С АВ), обозначается символически (АВС); если этой плоскостью является плоскость б, то пишут б = (АВС) или (АВС)= б. Стол, имеющий три ножки, не может качаться на плоском полу. Его устойчивость объясняется тем, что концы трех его ножек (три точки) принадлежат одной плоскости - плоскости пола, но не принадлежат одной прямой. Плохо сделанный стол на четырех ножках качается на плоском полу, и под одну из его ножек что-нибудь стараются подложить.

Прямой и точкой, не лежащей на прямой.

По теореме 1 через любую прямую и не принадлежащую ей точку можно провести плоскость, и притом только одну.

Теорема 2. Через любые две пересекающиеся прямые можно провести плоскость, и притом только одну.

Если прямая проходит через две точки плоскости, то она лежит в этой плоскости

Теорема 3. Через две параллельные прямые можно провести единственную плоскость.

Здесь из принятых нами аксиом стереометрии мы получим важные теоремы и следствия о прямых и плоскостях. Сами по себе они достаточно очевидны. Рассмотрим их доказательства, которые показывают, как какое-либо утверждение можно строго вывести из аксиом со всеми необходимыми ссылками.

2.1 Задание прямой двумя точками

Доказательство. В п. 1.1 уже доказано, что через каждые две точки А, В проходит прямая а.

Докажем, что эта прямая только одна. Прямая а лежит в некоторой плоскости а. Допустим, что, кроме прямой а, через точки А, В проходит ещё прямая b (рис. 31). По аксиоме 3 прямая, имеющая с плоскостью две общие точки, лежит в этой плоскости. Так как прямая b имеет с а общие точки А и B, то b лежит в плоскости α.

Рис. 31

Но в плоскости а выполняется планиметрия, и, следовательно, через две точки А и B проходит только одна прямая. Значит, прямые а и b совпадают. Таким образом, через точки А и В проходит только одна прямая.

Следствие. В пространстве (как и на плоскости) две различные прямые не могут иметь более одной общей точки.

Две прямые, имеющие единственную общую точку, называются пересекающимися.

Замечание. Не всегда предложение, справедливое в планиметрии, верно и в стереометрии. Так, например, в плоскости через две данные точки N, S проходит лишь одна окружность с диаметром NS, а в пространстве таких окружностей бесконечное множество - в каждой плоскости, проходящей через точки N, S, лежит такая окружность (рис. 32, а).

Рис. 32

Но прямая, проходящая через точки N, S в пространстве, лишь одна. Эта общая прямая всех плоскостей, проходящих через точки N, S (рис. 32, б).

Доказав, что в пространстве через каждые две точки проходит единственная прямая, мы можем задавать прямую в пространстве любой парой её точек, не заботясь о том, в какой плоскости эта прямая лежит. Прямая, проходящая через точки А, B, обозначается (АВ).

Аналогичное верно и для отрезков: каждые две точки в пространстве служат концами единственного отрезка.

2.2 Задание плоскости тремя точками

Доказательство. Пусть точки А, B, С не лежат на одной прямой. По аксиоме плоскости через эти точки проходит некоторая плоскость а (см. рис. 6). Докажем, что она только одна.

Допустим, что через точки А, B, С проходит ещё одна плоскость (3, отличная от а. Плоскости а и р имеют общие точки (например, точку А). По аксиоме 2 пересечением плоскостей α и β является их общая прямая. На этой прямой лежат все общие точки плоскостей α и β, а значит, точки A, B, С. Но это противоречит условию теоремы, так как согласно ему A, B, С не лежат на одной прямой. Итак, через точки А, В, С проходит лишь одна плоскость α.

Плоскость, проходящую через три точки А, В, С, не лежащие на одной прямой, обозначают (ABC).

Легко проиллюстрировать теорему 2. Например, положение двери фиксируется двумя дверными петлями и замком.

2.3 Задание плоскости прямой и точкой и двумя прямыми

Доказательство. Пусть даны прямая а и не лежащая на ней точка А. Возьмём на прямой а две точки B и С (рис. 33). Точка А не лежит с ними на одной прямой, так как через точки B и С проходит лишь одна прямая - это прямая а, а точка А не лежит на ней по условию теоремы.

Рис. 33

Через точки А, B, С, не лежащие на одной прямой, проходит (по теореме 2) единственная плоскость АBС. Прямая а имеет с ней две общие точки B и С и, значит, по аксиоме 3 лежит в ней. Таким образом, плоскость АBС и есть плоскость, проходящая через прямую а и точку А.

Единственность такой плоскости докажем способом от противного.

Пусть есть ещё одна плоскость β, содержащая прямую а и точку А. Тогда она содержит точки B и С. По теореме 2 она должна совпадать с плоскостью АBС. Полученное противоречие и доказывает единственность.

Вот иллюстрация этой теоремы: поворачивая переплёт книги, вы в каждый момент пальцами фиксируете его положение.

Доказательство. Пусть прямые а и b пересекаются в точке А. Возьмём на прямой b другую точку B (рис. 34). По теореме 3 через прямую а и точку В проходит плоскость а. Согласно аксиоме 3 прямая Ь лежит в этой плоскости, так как имеет с ней две общие точки А и В. Значит, плоскость а проходит через прямые а и b. Единственность такой плоскости докажите самостоятельно способом от противного.

Рис. 34

Теперь мы знаем три способа задания плоскости:

1. тремя точками, не лежащими на одной прямой;
2. прямой и не лежащей на ней точкой;
3. двумя пересекающимися прямыми.

Вопросы для самоконтроля

1. Какие вы знаете способы задания прямой в пространстве?
2. Какие вы знаете способы задания плоскости?