Методи за определяне на равнина върху диаграма. Методи за дефиниране на равнина в чертеж Методи за дефиниране и свойства на числови равнини

5.1 Настройка на равнината

Равнината се определя от три произволни точки, които не принадлежат на една права. Равнината в пространството може да бъде определена:

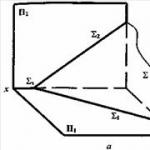
· три точки, които не лежат на една и съща права линия (Фигура 5.1, А);

· права линия и точка, която не й принадлежи (Фигура 5.1, b);

· две пресичащи се прави линии (Фигура 5.1, V);

· две успоредни прави линии (Фигура 5.1, Ж);

· всяка плоска фигура (Фигура 5.1, д).

Фигура 5.1

Всеки от изброените методи за уточняване на равнина позволява преход към всеки друг, т.к позицията на правата в равнината се определя от нейните две точки или една точка и посоката на тази права.

Често се използва методът за определяне на равнина с помощта на прави линии (взаимно пресичащи се или успоредни), по които тази равнина се пресича с проекционните равнини P 1 P 2, P 3. Освен това - Това е дефиницията на равнина със следи, като същевременно се запазва яснотата на изображението (Фигура 5.2).

Фигура 5.2

5.2 Следи от самолет.

Линията на пресичане на разглежданата равнина с проекционната равнина (P 1 , P 2, P 3 ) наречена следа от самолета. С други думи, следата на една равнина е права линия, лежаща в проекционната равнина. Следата се присвоява името на проекционната равнина, към която принадлежи. Например, хоризонтална следа се получава, когато дадена равнина се пресича с равнина P 1 и се обозначава, фронтална - с равнина P 2 (), профил - с равнина P 3 (). Две следи от една и съща равнина се пресичат върху проекционната ос в точка, наречена точка на изчезване на следите. Всяка от следите на равнината съвпада с нейната едноименна проекция, останалите проекции се оказват лежащи върху осите. Например хоризонталната следа на равнината Σ (Фигура 5.2) съвпада с нейната хоризонтална проекция, нейната фронтална проекция е върху оста х, а профилът по оста u.По местоположението на следите на равнината може да се прецени позицията на тази равнина в пространството спрямо проекционните равнини P 1, P 2, P 3.

5.3 Разположение на равнината спрямо проекционните равнини

Всяка равнина, произволно взета в пространството, може да заема общо или конкретно положение. Обща равнина е равнина, която не е перпендикулярна на никоя от проекционните равнини (виж Фигура 5.2). Всички останали равнини (с изключение на проекционните равнини) принадлежат към равнините на определена позиция и се разделят на проекционни равнини и равнини на ниво. |Проектираща равнина е равнина, перпендикулярна на единица
от проекционни равнини. Например хоризонталната проекционна равнина е перпендикулярна на хоризонталната проекционна равнина P 1 (Фигура 5.3).

Фигура 5.3

Хоризонталните проекции на всички геометрични изображения (точки, линии, фигури), лежащи в тази равнина, съвпадат с хоризонталната следа 1. Ъгълът, който се образува между равнините и P 2, се проектира върху P 1 без изкривяване. Фронтална следа 2 е перпендикулярна на оста x.

Равнината на фронталната проекция () е перпендикулярна на фронталната равнина P 2, показана на фигура 5.4. Фронталните проекции на всички геометрични изображения (точки, линии, фигури), лежащи в тази равнина, съвпадат с фронталната следа на равнина 2. Ъгълът, който се образува между дадената равнина и P 1, се проектира върху P 2 без изкривяване. Хоризонталната следа на равнина 1 е перпендикулярна на оста x.

Фигура 5.4

Равнината на проекция на профила T (T 1, T 2) е перпендикулярна на равнината на проекцията на профила P 3 (Фигура 5.5).

Фигура 5.5

Профилните проекции на всички геометрични изображения (точки, линии, фигури), лежащи в тази равнина, съвпадат с профилната следа на равнината T 3 . Ъгли и , които се образуват между дадена равнина и равнините на проекциите P 1 и P 2 (= T^P 1 ; = T^P 2 ), проектиран върху равнината P 3 без изкривяване. Хоризонталните и фронталните следи на равнината са успоредни на оста Х.

Равнината, проектираща профила, може да минава през оста x: (Фигура 5.6).

Фигура 5.6

Следите на тази равнина 1 = 2 съвпадат една с друга и с оста x, така че не определят позицията на равнината. В допълнение към следите е необходимо да се посочи точка в равнината (Фигура 5.6). В конкретен случай тази равнина може да бъде ъглополовяща. Ъгъл ° = °, а точката А е на еднакво разстояние от проекционните равнини P 1 и P 2 . Равнина на ниво е равнина, която е едновременно перпендикулярна на две проекционни равнини и успоредна на трета. Има три вида такива самолети (Фигура 5.7):

· хоризонталната равнина на нивото е перпендикулярна на P 2, P 3 и успоредна на P 1 (Фигура 5.7, А);

· фронталната равнина на нивото е перпендикулярна на P 1, P 3 и успоредна на P 2 (Фигура 5.7, б);

· профилната равнина на нивото е перпендикулярна на P 1, P 2 и успоредна на P 3 (Фигура 5.7 V).

Фигура 5.7

От дефиницията на равнините на нивото следва, че една от проекциите на точка, линия, фигура, принадлежаща на тези равнини, ще съвпадне със следата на едноименната равнина на нивото, а другата проекция ще бъде естественият размер на тези геометрични изображения.

5.4 Признаци за принадлежност на точка и права равнина

За да определите дали дадена точка принадлежи на права равнина, разположена в пространството, трябва да се ръководите от следните разпоредби:

· точка принадлежи на равнина, ако през нея може да се прекара права, лежаща в равнината;

· права принадлежи на равнина, ако има поне две общи точки с равнината;

· правата принадлежи на равнина, ако минава през точка от дадена равнина, успоредна на права, принадлежаща на тази равнина.

През една точка на равнината могат да бъдат начертани безкраен брой прави. Това могат да бъдат произволни линии и линии, които заемат специално положение по отношение на проекционните равнини P 1 P 2, P 3 . Права линия, принадлежаща на разглежданата равнина, начертана успоредно на хоризонталната равнина на проекциите, се нарича r хоризонталносамолет.

Права линия, принадлежаща на разглежданата равнина, начертана успоредно на фронталната равнина на проекциите, се нарича челенсамолет.

Хоризонталните и предните линии са равни линии.

Хоризонталната равнина трябва да започне да се изгражда от фронталната проекция, т.к тя е успоредна на оста х, хоризонталната проекция на хоризонталата е успоредна на хоризонталната следа на равнината.

И тъй като всички хоризонтали на равнината са успоредни една на друга, можем да считаме хоризонталната следа на равнината за нулева хоризонтала (Фигура 5.8).

Предната част на самолета трябва да започне да се изгражда от хоризонтална проекция, т.к тя е успоредна на оста x, фронталната проекция на фронтала е успоредна на фронталната следа. Челната следа на самолета е нулева челна. Всички фронтове на равнината са успоредни един на друг (Фигура 5.9).

Фигура 5.8

Фигура 5.9

Линията на нивото включва също профилна права линия, разположена в дадена равнина и успоредна на P 3 .

Основните линии със специално положение в равнината, в допълнение към линията на нивото, включват линиите на най-големия наклон на равнината към равнината на проекцията.

5.5 Определяне на ъгъла на наклона на равнината спрямо проекционните равнини

Обща равнина, разположена произволно в пространството, е наклонена към проекционните равнини. За да се определи големината на двустенния ъгъл на наклона на дадена равнина към всяка проекционна равнина, се използват линиите на най-големия наклон на равнината към проекционната равнина: до P 1 - линията на наклона, до P 2 - линията на най-големият наклон на равнината към равнината П 2.

Линиите с най-голям наклон на равнината са прави линии, които образуват най-голям ъгъл с равнината на проекцията и са начертани в равнината, перпендикулярна на съответната линия на нивото. Линията с най-голям наклон и съответната й проекция образуват линеен ъгъл, който измерва стойността на двустенния ъгъл, образуван от тази равнина и равнината на проекциите (Фигура 5.10).

Положението на една равнина в пространството се определя от нейните три точки, които не лежат на една права линия. Следователно, за да се определи равнина върху диаграма, е достатъчно да се уточнят три нейни точки (фиг. 206). Равнината може да бъде определена от точка и права (фиг. 207, а), две успоредни прави (фиг. 207, б), две пресичащи се прави (фиг. 207, в), триъгълник (фиг. 207). , д).

Можете да дефинирате равнина със следи. Следата на равнината е правата линия, по която тази равнина пресича равнината на проекцията. На фиг. 208 Pv - фронтална следа от равнина P, Рн - хоризонтална следа от равнина P, Pw - профилна следа от равнина P.

Различни случаи на разположение на равнини спрямо проекционни равнини

Общ самолет - равнина, разположена наклонено към всички проекционни равнини (фиг. 208). Такава равнина се пресича с три проекционни равнини по прави линии, които са следи от тази равнина. Всяка двойка следи се събира в точка, наречена точка на изчезване на равнинните следи и е разположена върху оста на проекцията. Равнината на обща позиция има три точки на изчезване, които са обозначени с Px, Py, Pz. В тези точки равнината пресича координатните оси. Равнинните фигури, лежащи в обща равнина, се проектират с изкривяване.

Проекционна равнина - равнина, перпендикулярна на която и да е проекционна равнина.

Хоризонтална проекционна равнина - равнина, перпендикулярна на хоризонталната равнина на проекциите Н (фиг. 209).

Равнина на фронтална проекция - равнина, перпендикулярна на фронталната равнина на проекция (фиг. 210).

Профилно-проектираща равнина - равнина, перпендикулярна на профилната равнина на проекциите (фиг. 211).

Проекционната равнина се проектира върху проекционната равнина, на която е перпендикулярна на права линия. Па фиг. 209 равнина P се проектира хоризонтално, ΔАВС, лежаща в равнината P, се проектира в отсечка с права линия, която съвпада със следата на равнината Рн. На фиг. 210 ΔDEF, принадлежащ на фронтално изпъкналата равнина R, се проектира в отсечка, съвпадаща със следата на равнината Rv. На фиг. 211 ΔKMN, лежаща в равнината Q, проектираща профила, се проектира върху равнината W в сегмент, съвпадащ със следата на равнината Qw. Поради това проекционните равнини често се използват като спомагателни равнини в различни конструкции. Например, за да начертаете хоризонтално проектирана равнина през права AB (фиг. 212), достатъчно е да начертаете хоризонтална следа от тази равнина през хоризонталната проекция на права AB, тъй като всичко, което лежи в тази равнина, включително права AB , се проектира върху неговата хоризонтална пътека. Фронталната следа на фронтално изпъкналата равнина съвпада с фронталната проекция на права a"b" (фиг. 213). Следите на проектиращите равнини върху други проекционни равнини са перпендикулярни на съответните проекционни оси (виж Фиг. 209, 210, 211).

Ориз. 212 Фиг. 213

Равнините, перпендикулярни на две проекционни равнини, са успоредни на третата проекционна равнина . Геометричните фигури, лежащи в тези равнини, се проектират без изкривяване върху проекционната равнина, на която тази равнина е успоредна (фиг. 214, 215; 216). Такива равнини се наричат същите като проекционната равнина, успоредна на която са разположени: хоризонтална равнина (фиг. 214), фронтална равнина (фиг. 215), профилна равнина (фиг. 216).

В планиметрията самолетът е една от основните фигури, следователно е много важно да имате ясно разбиране за него. Тази статия е създадена, за да покрие тази тема. Първо се дава концепцията за равнина, нейното графично представяне и се показват обозначенията на равнините. След това равнината се разглежда заедно с точка, права линия или друга равнина и опциите произтичат от относителните им позиции в пространството. Във втория, третия и четвъртия параграф на статията са анализирани всички опции за взаимното разположение на две равнини, права линия и равнина, както и точки и равнини, дадени са основните аксиоми и графични илюстрации. В заключение са дадени основните методи за определяне на равнина в пространството.

Навигация в страницата.

Равнина – основни понятия, символи и изображения.

Най-простите и основни геометрични фигури в триизмерното пространство са точка, права линия и равнина. Вече имаме представа за точка и права на равнина. Ако поставим равнина, върху която са изобразени точки и прави в триизмерното пространство, тогава получаваме точки и прави в пространството. Идеята за равнина в пространството ни позволява да получим например повърхността на маса или стена. Масата или стената обаче има крайни размери и равнината се простира отвъд нейните граници до безкрайност.

Точките и линиите в пространството се обозначават по същия начин, както в равнината - съответно с големи и малки латински букви. Например точки A и Q, прави a и d. Ако са дадени две точки, лежащи на права, тогава правата може да бъде означена с две букви, съответстващи на тези точки. Например права линия AB или BA минава през точки A и B. Самолетите обикновено се обозначават с малки гръцки букви, например самолети или.

При решаването на задачи става необходимо да се изобразят равнини на чертеж. Равнината обикновено се изобразява като успоредник или произволна проста затворена област.

Равнината обикновено се разглежда заедно с точки, прави линии или други равнини и възникват различни варианти за тяхното взаимно разположение. Нека да преминем към тяхното описание.

Относителното положение на равнината и точката.

Да започнем с аксиомата: във всяка равнина има точки. От него следва първият вариант за взаимното разположение на равнината и точката - точката може да принадлежи на равнината. С други думи, една равнина може да премине през точка. За да се посочи, че дадена точка принадлежи на равнина, се използва символът "". Например, ако равнината минава през точка А, тогава можете накратко да напишете .

Трябва да се разбере, че на дадена равнина в пространството има безкрайно много точки.

Следната аксиома показва колко точки в пространството трябва да бъдат отбелязани, за да определят определена равнина: през три точки, които не лежат на една права, минава равнина, и то само една. Ако са известни три точки, лежащи в една равнина, тогава равнината може да се означи с три букви, съответстващи на тези точки. Например, ако една равнина минава през точки A, B и C, тогава тя може да бъде обозначена като ABC.

Нека формулираме друга аксиома, която дава втората версия на взаимното разположение на равнината и точката: има поне четири точки, които не лежат в една и съща равнина. Така че точка в пространството може да не принадлежи на равнината. Действително, по силата на предишната аксиома, една равнина минава през три точки в пространството и четвъртата точка може или не може да лежи на тази равнина. Когато пишете кратко, използвайте символа „”, което е еквивалентно на фразата „не принадлежи”.

Например, ако точка А не лежи в равнината, тогава използвайте кратка нотация.

Права и равнина в пространството.

Първо, права линия може да лежи в равнина. В този случай поне две точки от тази права лежат в равнината. Това се установява от аксиомата: ако две точки от една права лежат в равнина, то всички точки от тази права лежат в равнината. За да запишете накратко принадлежността на дадена права към дадена равнина, използвайте символа “”. Например нотацията означава, че права линия a лежи в равнината.

Второ, права линия може да пресича равнина. В този случай правата и равнината имат една единствена обща точка, която се нарича пресечна точка на правата и равнината. Когато пиша накратко, обозначавам пресечната точка със символа „”. Например, нотацията означава, че права линия a пресича равнината в точка M. Когато равнина пресича определена права линия, възниква концепцията за ъгъл между правата и равнината.

Отделно, струва си да се съсредоточите върху права линия, която пресича равнината и е перпендикулярна на всяка права линия, лежаща в тази равнина. Такава права се нарича перпендикулярна на равнината. За кратко записване на перпендикулярността използвайте символа „”. За по-задълбочено изучаване на материала можете да се обърнете към статията перпендикулярност на права линия и равнина.

От особено значение при решаването на задачи, свързани с равнината, е така нареченият нормален вектор на равнината. Нормален вектор на равнина е всеки ненулев вектор, лежащ на права, перпендикулярна на тази равнина.

Трето, една права линия може да е успоредна на равнината, тоест да няма общи точки в нея. Когато пишете едновременност накратко, използвайте символа „“. Например, ако права a е успоредна на равнината, тогава можем да напишем . Препоръчваме ви да проучите този случай по-подробно, като се позовавате на статията паралелизъм на права и равнина.

Трябва да се каже, че права линия, лежаща в равнина, разделя тази равнина на две полуравнини. Правата в този случай се нарича граница на полуравнините. Всякакви две точки от една и съща полуравнина лежат от една и съща страна на права, а две точки от различни полуравнини лежат от противоположните страни на граничната линия.

Взаимно разположение на равнините.

Две равнини в пространството могат да съвпадат. В този случай те имат поне три общи точки.

Две равнини в пространството могат да се пресичат. Пресечната точка на две равнини е права линия, която се установява от аксиомата: ако две равнини имат обща точка, то те имат обща права линия, на която лежат всички общи точки на тези равнини.

В този случай възниква концепцията за ъгъл между пресичащи се равнини. От особен интерес е случаят, когато ъгълът между равнините е деветдесет градуса. Такива равнини се наричат перпендикулярни. Говорихме за тях в статията перпендикулярност на равнините.

И накрая, две равнини в пространството могат да бъдат успоредни, тоест да нямат общи точки. Препоръчваме ви да прочетете статията паралелност на равнините, за да получите пълно разбиране на тази опция за относителното разположение на равнините.

Методи за определяне на равнина.

Сега ще изброим основните начини за определяне на конкретна равнина в пространството.

Първо, една равнина може да бъде определена чрез фиксиране на три точки в пространството, които не лежат на една и съща права линия. Този метод се основава на аксиомата: през всеки три точки, които не лежат на една права, има една равнина.

Ако една равнина е фиксирана и определена в триизмерното пространство чрез посочване на координатите на нейните три различни точки, които не лежат на една и съща права линия, тогава можем да напишем уравнението на равнината, минаваща през трите дадени точки.

Следващите два метода за дефиниране на равнина са следствие от предишния. Те се основават на следствия от аксиомата за равнина, минаваща през три точки:

равнина минава през права и точка, която не лежи върху нея, и само една (виж също статията уравнение на равнина, минаваща през права и точка);
Има само една равнина, минаваща през две пресичащи се прави (препоръчваме ви да прочетете материала в статията: уравнение на равнина, минаваща през две пресичащи се прави).

Четвъртият начин за дефиниране на равнина в пространството се основава на дефиниране на успоредни прави. Припомнете си, че две прави в пространството се наричат успоредни, ако лежат в една равнина и не се пресичат. Така, като посочим две успоредни прави в пространството, ще определим единствената равнина, в която лежат тези прави.

Ако една равнина е дадена по посочения начин в триизмерно пространство спрямо правоъгълна координатна система, тогава можем да създадем уравнение за равнина, минаваща през две успоредни прави.

В уроците по геометрия в гимназията се доказва следната теорема: през фиксирана точка в пространството минава една равнина, перпендикулярна на дадена права. По този начин можем да дефинираме равнина, ако посочим точката, през която тя минава, и линия, перпендикулярна на нея.

Ако правоъгълна координатна система е фиксирана в триизмерното пространство и равнина е зададена по посочения начин, тогава е възможно да се построи уравнение за равнина, минаваща през дадена точка, перпендикулярна на дадена права линия.

Вместо линия, перпендикулярна на равнината, можете да посочите един от нормалните вектори на тази равнина. В този случай е възможно да се пише

Въведение

От курса по планиметрия знаем, че равнината е множество, чиито елементи са точки и в което е изпълнена системата от планиметрични аксиоми, описващи свойствата на точките и правите.

Пространството е множество, чиито елементи са точки и в което е изпълнена системата от аксиоми на стереометрията, описваща свойствата на точки, прави и равнини. Системата от аксиоми на стереометрията дава описание на свойствата на пространството и неговите основни елементи. Понятията „точка“, „права линия“ и „равнина“ се приемат без дефиниции: тяхното описание и свойства се съдържат в аксиомите. От друга страна, понятията „точка“, „права“, „равнина“ имат ясно значение, отразено в чертежите и чертежите.

Изучаването на пространството води до необходимостта от разширяване на системата от аксиоми на планиметрията и разглеждане на нова група аксиоми, които изразяват свойствата на относителните позиции на точки, прави линии и равнини, което е особено важно за нас в космоса.

Целта на резюмето е да се получи ясна представа за пространството и начините за подреждане на равнини в пространството.

За постигането на тази цел се поставят следните задачи:

- обмислете начини за определяне на равнини в пространството,
- разгледайте основните аксиоми на стереометрията;
- изучаване на възможни варианти за относителното разположение на равнините в пространството,
- формулират основните характеристики и свойства на относителното разположение на равнините в пространството;

Методи за определяне на равнина

Изследването на пространството води до необходимостта от разширяване на системата от аксиоми.

Нека разгледаме аксиома R1. В космоса има самолети. Във всяка равнина на пространството са изпълнени всички аксиоми на планиметрията. Тази аксиома ни дава право да разглеждаме във всяка равнина на пространствените сегменти правите линии с всичките им свойства, които са изучавани в планиметрията. Например, ако права линия a и точка M, която не й принадлежи, лежат в някаква равнина b, тогава в тази равнина е възможно да се начертае през точка M права линия, успоредна на права a, и освен това само една.

Аксиома R3 казва: каквато и да е равнината, има точки, които принадлежат на тази равнина, и точки, които не й принадлежат. Тази аксиома гласи, че за всяка равнина в пространството можете да изберете произволен брой точки в тази равнина, както и произволен брой точки извън нея. Ако точка A лежи в (принадлежи на) равнина b, тогава напишете: A b и кажете, че равнината b минава през точка A. Ако точка A не принадлежи на равнина b, тогава напишете: A b и кажете, че равнината b не преминава през точка А.

Една равнина в пространството е еднозначно определена:

Три точки, които не лежат на права линия. Аксиома R2 (аксиома за равнина) гласи: През всеки три точки, които не принадлежат на една права, може да се начертае равнина и то само една. Равнина, която минава през точки A, B и C, които не принадлежат на една и съща права (C AB), се обозначава символично (ABC); ако тази равнина е равнина b, тогава напишете b = (ABC) или (ABC) = b. Маса с три крака не може да се люлее на равен под. Неговата стабилност се обяснява с факта, че краищата на трите му крака (три точки) принадлежат на една равнина - равнината на пода, но не принадлежат на една права линия. Лошо направена маса с четири крака се люлее на равния под и те се опитват да подложат нещо под единия й крак.

Права линия и точка, която не лежи на права линия.

Според теорема 1 през всяка права линия и точка, която не й принадлежи, може да се начертае равнина и то само една.

Теорема 2. През всеки две пресичащи се прави можете да начертаете равнина и само една.

Ако права линия минава през две точки от равнина, то тя лежи в тази равнина

Теорема 3. През две успоредни прави може да се прекара единствена равнина.

Тук, от аксиомите на стереометрията, които сме приели, ще получим важни теореми и следствия за прави линии и равнини. Сами по себе си те са доста очевидни. Нека разгледаме техните доказателства, които показват как всяко твърдение може да бъде строго изведено от аксиомите с всички необходими препратки.

2.1 Определяне на права линия с две точки

Доказателство. В параграф 1.1 вече беше доказано, че през всеки две точки A, B минава права a.

Нека докажем, че има само една линия. Правата a лежи в определена равнина a. Да приемем, че освен права a през точки A и B минава и права b (фиг. 31). Според аксиома 3 в тази равнина лежи права, която има две общи точки с равнина. Тъй като правата b има общи точки A и B с a, тогава b лежи в равнината α.

Ориз. 31

Но в равнина a се извършва планиметрия и следователно само една права линия минава през две точки A и B. Това означава, че правите a и b съвпадат. Така само една права линия минава през точки A и B.

Последица. В пространството (както и в равнината) две различни прави не могат да имат повече от една обща точка.

Две прави, които имат една обща точка, се наричат пресичащи се.

Коментирайте. Едно твърдение, което е валидно в планиметрията, не винаги е вярно в стереометрията. Така например в равнина през две дадени точки N, S минава само една окръжност с диаметър NS, а в пространството на такива окръжности има безкраен брой - във всяка равнина, минаваща през точките N, S, лежи такъв кръг (фиг. 32, а) .

Ориз. 32

Но има само една права линия, минаваща през точки N, S в пространството. Това е общата права линия на всички равнини, минаващи през точки N, S (фиг. 32, b).

След като доказахме, че има една права линия, минаваща през всеки две точки в пространството, можем да определим права линия в пространството с всяка двойка нейни точки, без да се притесняваме за равнината, в която лежи тази права линия. Правата, минаваща през точки A, B, се обозначава (AB).

Същото важи и за сегментите: всеки две точки в пространството служат като краища на един сегмент.

2.2 Определяне на равнина с три точки

Доказателство. Нека точките A, B, C не лежат на една права. Според аксиомата за равнината през тези точки минава определена равнина a (виж фиг. 6). Нека докажем, че има само един.

Да приемем, че друга равнина (3, различна от a) минава през точки A, B, C. Равнините a и p имат общи точки (например точка A).Съгласно аксиома 2, пресечната точка на равнините α и β е тяхната обща права линия.В това отношение всички общи точки на равнините α и β лежат на една права линия и следователно точките A, B, C. Но това противоречи на условието на теоремата, тъй като според нея A, B, C правят не лежат на една и съща права.Така че през точките A,B,C минава само една равнина α.

Равнина, минаваща през три точки A, B, C, които не лежат на една и съща права линия, е обозначена (ABC).

Лесно е да се илюстрира теорема 2. Например, позицията на една врата се фиксира от две панти на вратата и ключалка.

2.3 Задаване на равнина с права и точка и две прави

Доказателство. Нека са дадени права a и нележаща на нея точка A. Да вземем две точки B и C на права a (фиг. 33). Точка A не лежи на една и съща права линия с тях, тъй като само една права линия минава през точки B и C - това е права линия a, а точка A не лежи върху нея според условията на теоремата.

Ориз. 33

През точки A, B, C, които не лежат на една и съща права, минава (по теорема 2) една равнина ABC. Правата a има две общи точки B и C с нея и следователно, съгласно аксиома 3, лежи в нея. Така равнината ABC е равнината, минаваща през права a и точка A.

Ще докажем уникалността на такава равнина от противното.

Нека има друга равнина β, съдържаща права a и точка A. Тогава тя съдържа точки B и C. Според теорема 2 тя трябва да съвпада с равнината ABC. Полученото противоречие доказва уникалност.

Ето една илюстрация на тази теорема: когато въртите подвързията на книга, вие всеки момент фиксирате позицията й с пръсти.

Доказателство. Нека правите a и b се пресичат в точка A. Вземете друга точка B на права b (фиг. 34). Според теорема 3 равнината a минава през права a и точка B. Съгласно аксиома 3 права b лежи в тази равнина, тъй като има две общи точки с нея A и B. Това означава, че равнина a минава през прави a и b. Докажете сами уникалността на такъв самолет от противното.