Let's say we have a line to which we need to set a perpendicular, i.e. another line at an angle of 90 degrees relative to the first. Or we have an angle (for example, the corner of a room) and we need to check if it is equal to 90 degrees.
All this can be done with just a tape measure and a pencil.
There are two great things like " egyptian triangle”and the Pythagorean theorem, which will help us with this.
The first lines that come to a person's imagination are straight lines and a circle. With them is born a geometry whose name, literally measuring the earth, clearly indicates the purpose for which they were directed. Agridensors were the first geometers of antiquity. ancient egypt. The Greeks give them the name arpedonapti, ropes of ropes. By pulling the ropes, Egyptian geometers could trace circles from right to right, the operation of which remains traced in many modern languages, in the expression "draw a line". The use of strings for field operations has remained unchanged for many centuries and is in the work of the agrimensor even in relatively recent times.
So, egyptian triangle is a right triangle with the ratio of all sides equal to 3:4:5 (leg 3: leg 4: hypotenuse 5).
The Egyptian triangle is directly related to the Pythagorean theorem - the sum of the squares of the legs is equal to the square of the hypotenuse (3*3 + 4*4 = 5*5).
How can this help us? Everything is very simple.
Task number 1. You need to draw a perpendicular to a straight line (for example, a line at 90 degrees to a wall).
The testimonies of Greek historians want geometry to be born in Egypt. If a river landed somewhere, a landowner who came to the king told him about this incident: he then sent officers who observed and measured how much the land had become smaller, so that in the future the payer would pay tribute in proportion. If the river had just cleared the borders of the camps, then it would have been necessary for the same officials to restore the correct divisions.
Egyptian farmers were called "arpedonapti", rope kivas. And pulling the ropes, they traced the two simplest and most important lines of geometry: the straight line and the circle. The first, by simply pulling the rope between two points, "whose operation is still" image in the expressions "pulling straight", "pulling perpendicular"; secondly, by turning one of them around the rest, which remains motionless. Is it conceivable that the richness of the building could lead to these two elemental practices?
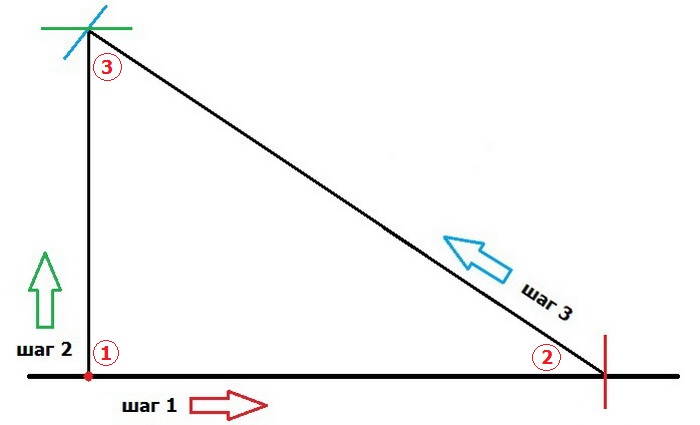Step 1. To do this, from point No. 1 (where our corner will be) you need to measure on this line any distance that is a multiple of three or four - this will be our first leg (equal to three or four parts, respectively), we get point No. 2.
For ease of calculation, you can take a distance, for example 2m (these are 4 parts of 50cm each).
Today it is natural to regard the leaf as a natural geometry, which we perceive as the exclusive use of the line and compass as an arbitrary limitation imposed by speculative spirits, preferring the narrowness of the number of axioms to the conveniences associated with a multitude of tools; so that theoretical geometry - here, of course, classical, Euclidean geometry - certainly distinguishes itself from the technique-attacking architect, especially because the former voluntarily excludes the use of tools, commands, pantographs, which use the latter to their advantage.
Step 2. Then, from the same point No. 1, we measure 1.5 m (3 parts of 50 cm each) up (set an approximate perpendicular), draw a line (green).
Step 3. Now from point number 2 you need to put a mark on the green line at a distance of 2.5m (5 parts of 50cm). The intersection of these marks will be our point number 3.
By connecting points No. 1 and No. 3, we get a line perpendicular to our first line.
In doing so, we completely neglect the "field" geometry in favor of this "on paper", and we see that in order to transfer to the ground, geometric operations need different methods, sometimes completely from those that had been taken on a narrow sheet scale. Not to mention the fact that the accuracy of the drawing is much more important on the ground than on paper. All an architect who clearly stated the general project and is mindful of the goals that led him to design may well be a rough design, cadastral maps, and not just antiquities, which were necessarily designed with means and rudimentary supports, relative to modern times, do not reproduce exactly field boundaries.
Task number 2. Second situation- there is an angle and you need to check whether it is straight.
Here it is, our corner. It's much easier to check with a large square. And if he is not?
Everyone who listened attentively to a geometry teacher at school is very familiar with what the Egyptian triangle is. It differs from other types of similar ones with an angle of 90 degrees by a special aspect ratio. When a person first hears the phrase "Egyptian triangle", pictures of majestic pyramids and pharaohs come to mind. And what does history say?
It is possible that, as an error of a few percent, the minimum that can occur when reproducing a non-small scale will lead to an absolute error in this area, which is unlikely to be acceptable. In these cases, it is necessary to know information about the shape and dimensions of the described object, and then the task of geometry is to restore the missing accuracy of the map to the ground. Doesn't help in demos. For precision in field operations, paper geometry replaces mental process geometry.
In the backward passage from logical precision to material resulting from the expansion of the scale needed to move from design to implementation, the rope trend remains one of the main operations far beyond Egyptian antiquity and classical Greece. almost unchanged in the "modern era, it is exceeded in some respects only from" the invention and from the processing of optical instruments. and while on paper the perpendicular is easily achieved by the use of line and commands, the same operation on the ground requires that it must be carried out with some precision by radically different procedures.
As is always the case, there are several theories regarding the name "Egyptian triangle". According to one of them, the well-known Pythagorean theorem saw the light precisely because of this figure. In 535 BC. Pythagoras, following the recommendation of Thales, went to Egypt in order to fill in some gaps in the knowledge of mathematics and astronomy. There he drew attention to the peculiarities of the work of Egyptian surveyors. They built in a very unusual way with a right angle, the sides of which were interconnected with one another in a 3-4-5 ratio. This mathematical series made it relatively easy to connect the squares of all three sides with one rule. This is how the famous theorem arose. And the Egyptian triangle is precisely the very figure that prompted Pythagoras to the most ingenious solution. According to other historical data, the Greeks gave the name to the figure: at that time they often visited Egypt, where they could be interested in the work of land surveyors. There is a possibility that, as is often the case with scientific discoveries, both stories happened at the same time, so it’s impossible to say with certainty who first came up with the name “Egyptian triangle”. Its properties are amazing and, of course, are not limited to the aspect ratio alone. Its area and sides are represented by whole numbers. Due to this, the application of the Pythagorean theorem to it allows us to obtain integer numbers of squares of the hypotenuse and legs: 9-16-25. Of course, this could just be a coincidence. But how, then, to explain the fact that the Egyptians considered "their" triangle sacred? They believed in its interconnection with the entire universe.
On the ground, the team does not need this because it is too small for the size of the pieces. It is also recognized that the team is perfectly at a right angle, the perpendicular it is able to track will be longer by more than a meter or so; If you want to build a square thirty or more meters to the side, you need to increase this meter line up to thirty times as much, an "imprecise operation" that probably does not give you better results than what you can get by looking at the eyes Straight corner.
These considerations bring us back to the original problem: what methods did the Egyptian Agrimans use to distinguish the squares of squares? How did they get the right angle? If this was a process followed by the ancient agridensors, it is not known that the Egyptians knew that a triangle of sides 3, 4 and 5 are rectangles, but even if they know about this or other Pythagorean triangles, the fact remains that this suggests knowledge of nature or, at least generation right angle.
After information about this unusual geometric figure became public, the world began searching for other similar triangles with integer sides. It was obvious that they existed. But the importance of the question was not just to perform mathematical calculations, but to test the "sacred" properties. The Egyptians, for all their unusualness, were never considered stupid - scientists still cannot explain exactly how the pyramids were built. And here, suddenly, a connection with Nature and the Universe was attributed to an ordinary figure. And, indeed, the found cuneiform contains indications of a similar triangle with a side whose size is described by a 15-digit number. Currently, the Egyptian triangle, the angles of which are 90 (right), 53 and 37 degrees, are found in completely unexpected places. For example, when studying the behavior of ordinary water molecules, it turned out that the change is accompanied by a restructuring of the spatial configuration of molecules, in which one can see ... the same Egyptian triangle. If we remember that it consists of three atoms, then we can talk about conditional three sides. Of course, we are not talking about the complete coincidence of the famous ratio, but the resulting numbers are very, very close to the desired ones. Is this why the Egyptians recognized their “3-4-5” triangle as a symbolic key to natural phenomena and the secrets of the Universe? After all, water, as you know, is the basis of life. Without a doubt, it is still too early to put an end to the study of the famous Egyptian figure. Science never rushes to conclusions, seeking to prove its assumptions. And we can only wait and be surprised by the knowledge
In the absence of partial documents and evidence, we are trying to solve the problem from a different point of view, turning it from a mathematician into a historical point of view. Let's ask: so "does this make a different angle?" Anyway, does the triangle have a special angle on sides 3, 4 and 5? So post. the question allows for an immediate answer: unlike the others, Pythagorean triangles, and in particular the simplest of them, sides 3, 4, and 5, can be matched by tilting one leg and then tilting again to the other. This creates a symmetrical configuration that fills everything available space without overlap and without gaps.
