The concept of equations with two variables is first formed in the course of mathematics for the 7th grade. Specific problems are considered, the process of solving which leads to this type of equations.
At the same time, they are studied quite superficially. The program focuses on systems of equations with two unknowns.
This has become the reason that problems in which certain restrictions are imposed on the coefficients of the equation are practically not considered. Not enough attention is paid to methods for solving tasks like "Solve an equation in natural or integer numbers." It is known that USE materials and entrance examination tickets often contain such exercises.
What kind of equations are defined as equations in two variables?
xy \u003d 8, 7x + 3y \u003d 13 or x 2 + y \u003d 7 are examples of equations with two variables.
Consider the equation x - 4y \u003d 16. If x \u003d 4 and y \u003d -3, it will be a correct equality. Hence, this pair of values is the solution of this equation.
The solution of any equation with two variables is the set of pairs of numbers (x; y) that satisfy this equation (turn it into a true equality).
Often the equation is transformed so that it can be used to obtain a system for finding unknowns.
Examples
Solve the equation: xy - 4 \u003d 4x - y.
In this example, you can use the factorization method. To do this, you need to group the terms and take the common factor out of brackets:
xy - 4 \u003d 4x - y;
xy - 4 - 4x + y \u003d 0;
(xy + y) - (4x + 4) = 0;
y(x + 1) - 4(x + 1) = 0;
(x + 1)(y - 4) = 0.
Answer: All pairs (x; 4), where x is any rational number and (-1; y), where y is any rational number.
Solve the equation: 4x 2 + y 2 + 2 = 2(2x - y).
The first step is grouping.
4x 2 + y 2 + 2 = 4x - 2y;
4x 2 + y 2 + 1 - 4x + 2y + 1 = 0;
(4x 2 - 4x + 1) + (y 2 + 2y + 1) = 0.
Applying the difference square formula, we get:
(2x - 1) 2 + (y + 1) 2 = 0.
When summing two non-negative expressions, zero will be obtained only if 2x - 1 \u003d 0 and y + 1 \u003d 0. It follows: x \u003d ½ and y \u003d -1.
Answer: (1/2; -1).
Solve the equation (x 2 - 6x + 10) (y 2 + 10y + 29) = 4.
It is rational to apply the evaluation method by highlighting the full squares in brackets.
((x - 3) 2 + 1) ((y + 5) 2 + 4) = 4.
Moreover, (x - 3) 2 + 1 ≥ 1, and (y + 5) 2 + 4 ≥ 4. Then the left side of the equation is always at least 4. Equality is possible in the case
(x - 3) 2 + 1 = 1 and (y + 5) 2 + 4 = 4. Hence x = 3, y = -5.
Answer: (3; -5).
Solve the equation in integers: x 2 + 10y 2 \u003d 15x + 3.
You can write this equation in this form:
x 2 \u003d -10y 2 + 15x + 3. If right side equals divided by 5, then 3 is the remainder. It follows from this that x 2 is not divisible by 5. It is known that the square of a number that is not divisible by 5 must give a remainder of either 1 or 4. This means that the equation has no roots.
Answer: There are no solutions.
Don't be discouraged by the difficulty in finding the right solution for an equation with two variables. Perseverance and practice will surely bear fruit.
In this article, we will learn how to solve biquadratic equations.
So, what kind of equations are called biquadratic?
All equations of the form ah 4+
bx
2
+
c
= 0
, where a ≠ 0, which are square with respect to x 2 , and are called biquadratic equations. As you can see, this entry is very similar to the quadratic equation, so we will solve biquadratic equations using the formulas that we used when solving the quadratic equation.
Only we will need to introduce a new variable, that is, we denote x 2 another variable, for example, at or t (or any other letter of the Latin alphabet).
For example, solve the equation x 4 + 4x 2 - 5 = 0.
Denote x 2
through at
(x 2 = y
) and get the equation y 2 + 4y - 5 = 0.
As you can see, you already know how to solve such equations.
We solve the resulting equation:
D \u003d 4 2 - 4 (- 5) \u003d 16 + 20 \u003d 36, √D \u003d √36 \u003d 6.
y 1 = (‒ 4 - 6)/2= - 10 /2 = - 5,
y 2 \u003d (- 4 + 6) / 2 \u003d 2 / 2 \u003d 1.
Let's go back to our variable x.
We got that x 2 \u003d - 5 and x 2 \u003d 1.
We note that the first equation has no solutions, and the second gives two solutions: x 1 = 1 and x 2 = –1. Be careful not to lose the negative root (most often they get the answer x = 1, which is not correct).
Answer:- 1 and 1.
To better understand the topic, let's look at a few examples.
Example 1 Solve the Equation 2x4 - 5x2 + 3 = 0.
Let x 2 \u003d y, then 2y 2 - 5y + 3 \u003d 0.
D = (‒ 5) 2 - 4 2 3 = 25 - 24 = 1, √D = √1 = 1.
y 1 \u003d (5 - 1) / (2 2) \u003d 4 / 4 \u003d 1, y 2 \u003d (5 + 1) / (2 2) \u003d 6 / 4 \u003d 1.5.
Then x 2 \u003d 1 and x 2 \u003d 1.5.
We get x 1 \u003d -1, x 2 \u003d 1, x 3 \u003d - √1.5, x 4 \u003d √1.5.
Answer: ‒1; 1; ‒ √1,5; √1,5.
Example 2 Solve the Equation 2 x 4 + 5 x 2 + 2 = 0.
2y 2 + 5y + 2 = 0.
D = 5 2 - 4 2 2 = 25 - 16 = 9, √D = √9 = 3.
y 1 = (– 5 – 3)/(2 2) = – 8/4 = –2, y 2 = (–5 + 3)/(2 2) = – 2/4 = – 0.5.
Then x 2 = - 2 and x 2 = - 0.5. Note that none of these equations has a solution.
Answer: there are no solutions.
Incomplete biquadratic equations- it is when b = 0 (ax 4 + c = 0) or else c = 0
(ax 4 + bx 2 = 0) are solved like incomplete quadratic equations.


Example 3 solve the equation x 4 - 25x 2 = 0
We factorize, take x 2 out of brackets and then x 2 (x 2 - 25) = 0.
We get x 2 \u003d 0 or x 2 - 25 \u003d 0, x 2 \u003d 25.
Then we have roots 0; 5 and - 5.
Answer: 0; 5; – 5.
Example 4 solve the equation 5x 4 - 45 = 0.
x 2 = - √9 (no solutions)
x 2 \u003d √9, x 1 \u003d - 3, x 2 \u003d 3.
As you can see, knowing how to solve quadratic equations, you can cope with biquadratic ones.
If you still have questions, sign up for my lessons. Tutor Valentina Galinevskaya.
site, with full or partial copying of the material, a link to the source is required.
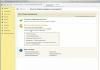
We offer you a convenient free online calculator to solve quadratic equations. You can quickly get and understand how they are solved, using understandable examples.
To produce solve quadratic equation online, first bring the equation to a general form:
ax2 + bx + c = 0
Fill in the form fields accordingly:
How to solve a quadratic equation
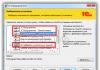
| How to solve a quadratic equation: | Root types: |
|
1.
Bring the quadratic equation to a general form: General view of Ax 2 +Bx+C=0 Example: 3x - 2x 2 +1=-1 Reduce to -2x 2 +3x+2=0 2.
We find the discriminant D. 3.
We find the roots of the equation. |
1.
Real roots. And. x1 is not equal to x2 The situation arises when D>0 and A is not equal to 0. 2.
The real roots are the same. x1 equals x2 3.
Two complex roots. x1=d+ei, x2=d-ei, where i=-(1) 1/2 5.
The equation has an infinite number of solutions. 6.
The equation has no solutions. |
To consolidate the algorithm, here are some more illustrative examples of solutions to quadratic equations.
Example 1. Solution of an ordinary quadratic equation with different real roots.
x 2 + 3x -10 = 0
In this equation
A=1, B=3, C=-10
D=B 2 -4*A*C = 9-4*1*(-10) = 9+40 = 49
Square root will be denoted as the number 1/2!
x1 \u003d (-B + D 1/2) / 2A \u003d (-3 + 7) / 2 \u003d 2
x2 \u003d (-B-D 1/2) / 2A \u003d (-3-7) / 2 \u003d -5
To check, let's substitute:
(x-2)*(x+5) = x2 -2x +5x - 10 = x2 + 3x -10
Example 2. Solving a quadratic equation with the same real roots.
x 2 - 8x + 16 = 0
A=1, B=-8, C=16
D \u003d k 2 - AC \u003d 16 - 16 \u003d 0
X=-k/A=4
Substitute
(x-4) * (x-4) \u003d (x-4) 2 \u003d X 2 - 8x + 16
Example 3. Solution of a quadratic equation with complex roots.
13x 2 - 4x + 1 = 0
A=1, B=-4, C=9
D \u003d b 2 - 4AC \u003d 16 - 4 * 13 * 1 \u003d 16 - 52 \u003d -36
The discriminant is negative - the roots are complex.
X1 \u003d (-B + D 1/2) / 2A \u003d (4 + 6i) / (2 * 13) \u003d 2/13 + 3i / 13
x2 \u003d (-B-D 1/2) / 2A \u003d (4-6i) / (2 * 13) \u003d 2 / 13-3i / 13
, where I is the square root of -1
Here are actually all possible cases of solving quadratic equations.
We hope that our online calculator will be very useful to you.
If the material was helpful, you can