Темата е взаимното разположение на две окръжности. Теория

Клас 7G, ​​Z

Тема на урока: „Относителното положение на две окръжности“
Цел: познаване на възможните случаи на взаимното разположение на две окръжности; прилагайте знания за решаване на проблеми.

Цели: Образователни: да се улесни създаването и консолидирането в учениците на визуално представяне на възможни случаи на подреждане на два кръга, учениците ще могат да:

Установява връзка между взаимното разположение на окръжностите, техните радиуси и разстоянието между центровете им;

Анализирайте геометричен дизайн и мислено го модифицирайте,

Развийте планиметрично въображение.

Студентите ще могат да прилагат теоретичните знания за решаване на проблеми.

Тип на урока: урок за въвеждане и затвърждаване на нови знания по материала.

Оборудване: презентация към урока; пергел, линийка, молив и учебник за всеки ученик.

Урок: . „Геометрия 7 клас”, Алмати „Атамура” 2012 г

По време на часовете.

Организиране на времето. Проверка на домашните.

3. Актуализиране на основни знания.

Повторете определенията за окръжност, кръг, радиус, диаметър, хорда, разстояние от точка до права линия.

1) 1) Какви случаи на местоположението на линия и окръжност знаете?

2) Коя права се нарича допирателна?

3) Коя права се нарича секанс?

4) Теорема за диаметъра, перпендикулярен на хордата?

5) Как е допирателната спрямо радиуса на окръжността?

6) Попълнете таблицата (на карти).

Учениците под ръководството на учителя решават и анализират задачи.

1) Правата a е допирателна към окръжност с център O. Ъгълът между допирателната и отсечката OA е 300. Намерете дължината на отсечката OA, ако радиусът е 2,5 m.

2) Определете относителната позиция на правата и окръжността, ако:

1. R=16cm, d=12cm 2. R=5cm, d=4.2cm 3. R=7.2dm, d=3.7dm 4. R=8 cm, d=1.2dm 5. R=5 cm, d= 50 мм

а) права линия и окръжност нямат общи точки;

б) правата е допирателна към окръжността;

в) права пресича окръжност.

d е разстоянието от центъра на окръжността до правата линия, R е радиусът на окръжността.

3) Какво може да се каже за взаимното разположение на правата и окръжността, ако диаметърът на окръжността е 10,3 cm, а разстоянието от центъра на окръжността до правата е 4,15 cm; 2 dm; 103 mm; 5,15 см, 1 дм 3 см.

4) Дадена е окръжност с център O и точка A. Къде се намира точка A, ако радиусът на окръжността е 7 cm и дължината на отсечката OA е: а) 4 cm; б) 10 cm; в) 70 mm.

4. Заедно с учениците разберете темата на урока и формулирайте целите на урока.

5. Въвеждане на нов материал.

Практическа работа в групи.

Изградете 3 кръга. За всяка окръжност построете друга окръжност така, че 1) 2 окръжности да не се пресичат, 2) 2 окръжности да се докосват, 3) две окръжности да се пресичат. Намерете радиуса на всяка окръжност и разстоянието между центровете на окръжностите, сравнете резултатите. Какво може да се заключи?
2) Обобщете и запишете в тетрадка случаите на взаимното разположение на две окръжности.

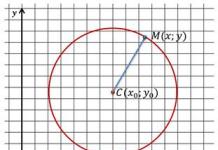
Относителното положение на две окръжности в равнина.

Окръжностите нямат общи точки (не се пресичат). (R1 и R2 са радиусите на окръжностите)

Ако R1 + R2< d,

d – Разстояние между центровете на окръжности.

в) Окръжностите имат две общи точки. (пресичат се).

Ако R1 + R2 > d,

Въпрос. Могат ли две окръжности да имат три общи точки?

6. Затвърдяване на изучения материал.

Намерете грешка в данните или изявлението и я коригирайте, като аргументирате мнението си:
А) Две окръжности се докосват. Техните радиуси са равни на R = 8 cm и r = 2 cm, разстоянието между центровете е d = 6.
Б) Две окръжности имат поне две общи точки.
B) R = 4, r = 3, d = 5. Окръжностите нямат общи точки.
D) R = 8, r = 6, d = 4. По-малкият кръг се намира вътре в по-големия.
Г) Два кръга не могат да бъдат разположени така, че единият да е вътре в другия.

7. Обобщение на урока. Какво научихте в урока? Какъв модел беше установен?

Как могат да бъдат разположени два кръга? В какъв случай окръжностите имат една обща точка? Как се нарича общата точка на две окръжности? Какви щрихи познавате? Кога окръжностите се пресичат? Какви окръжности се наричат ​​концентрични?

Тема на урока: " Относителното положение на две окръжности в равнина.

Мишена :

Образователни - усвояване на нови знания за взаимното разположение на две окръжности, подготовка за контролна работа

Развитие - развитие на изчислителни умения, развитие на логико-структурно мислене; развиване на умения за намиране на рационални решения и постигане на крайни резултати; развитие на познавателната активност и творческото мислене .

Образователни – формиране на отговорност и последователност у учениците; развитие на познавателни и естетически качества; формиране на информационна култура на учениците.

Поправителен - развиват пространствено мислене, памет, двигателни умения на ръцете.

Тип урок: изучаване на нов учебен материал, затвърдяване.

Тип урок: смесен урок.

Метод на обучение: словесно, визуално, практично.

Форма на обучение: колективен.

Средства за обучение: дъска

ПО ВРЕМЕ НА ЗАНЯТИЯТА:

1. Организационен етап

- поздравления;

- проверка на готовността за урока;

2. Актуализиране на основни знания.
Какви теми разгледахме в предишните уроци?

Общ вид на уравнението на окръжност?

Изпълнете устно:

Блиц анкета

3. Въвеждане на нов материал.

Каква цифра мислите, че ще разгледаме днес... Ами ако са двама??

Как могат да бъдат локализирани???

Децата показват с ръце (съседи) как могат да се подредят кръговете (физкултурна минута)

Е, какво мислите, че трябва да разгледаме днес?? Днес трябва да разгледаме относителната позиция на две окръжности. И разберете какво е разстоянието между центровете в зависимост от местоположението.

Тема на урока: « Относителното положение на два кръга. Разрешаване на проблем. »

1. Концентрични кръгове

2. Дизюнктни окръжности

3.Външен допир

4. Пресичащи се окръжности

5. Вътрешен допир

И така, нека заключим

4.Формиране на умения и способности

Намерете грешка в данните или изявлението и я коригирайте, като аргументирате мнението си:

А) Две окръжности се докосват. Техните радиуси са равни на R = 8 cm и r = 2 cm, разстоянието между центровете е d = 6.
Б) Две окръжности имат поне две общи точки.

B) R = 4, r = 3, d = 5. Окръжностите нямат общи точки.

D) R = 8, r = 6, d = 4. По-малкият кръг се намира вътре в по-големия.

Г) Два кръга не могат да бъдат разположени така, че единият да е в другия.

5. Затвърдяване на умения и способности.

Кръговете се допират външно. Радиусът на по-малката окръжност е 3 см. Радиусът на по-голямата окръжност е 5 см. Какво е разстоянието между центровете?

Решение: 3+5=8(cm)

Кръговете се допират вътрешно. Радиусът на по-малката окръжност е 3 см. Радиусът на по-голямата окръжност е 5 см. Какво е разстоянието между центровете на окръжностите?

Решение: 5-3=2(cm)

Кръговете се допират вътрешно. Разстоянието между центровете на окръжностите е 2,5 см. Какви са радиусите на окръжностите?

отговор: (5,5 см и 3 см), (6,5 см и 4 см) и т.н.

ПРОВЕРКА НА РАЗБИРАНЕТО

1) Как могат да бъдат разположени два кръга?

2) В какъв случай окръжностите имат една обща точка?

3) Как се нарича общата точка на две окръжности?

4) Какви докосвания знаете?

5) Кога се пресичат кръговете?

6) Какви окръжности се наричат ​​концентрични?

Допълнителни задачи по темата: Вектори. Координатен метод "(ако остане време)

1)E(4;12),Е(-4;-10), Ж(-2;6), з(4;-2) Намерете:

а) векторни координатиЕ.Ф., Г.Х.

б) дължина на вектораFG

в) координати на т. О - средатаЕ.Ф.

координати на точкиУ– средатаГ.Х.

г) уравнение на окръжност с диаметърFG

д) уравнение на праваFH

6. Домашна работа

& 96 № 1000. Кои от тези уравнения са уравнения на окръжност. Намерете център и радиус

7. Обобщаване на урока (3 мин.)

(дайте качествена оценка на работата на класа и отделните ученици).

8. Етап на рефлексия (2 минути.)

Нека са дадени окръжност и точка, която не съвпада с центъра й C (фиг. 205). Възможни са три случая: точката лежи вътре в окръжността (фиг. 205, a), върху окръжността (фиг. 205, b), извън окръжността (фиг. 205, c). Нека начертаем права линия, която ще пресича окръжността в точки K и L (в случай b) точката ще съвпадне с една от които ще бъде най-близо до точката в сравнение с всички останали точки на окръжността), а другата ще бъде най-отдалечен.

Така например на фиг. 205, а точка K от окръжността е най-близо до . Всъщност, за всяка друга точка от окръжността, начупената линия е по-дълга от сегмента SAG: но също така, напротив, за точка L намираме (отново начупената линия е по-дълга от сегмента на правата линия). Анализът на останалите два случая оставяме на читателя. Обърнете внимание, че най-голямото разстояние е равно на най-малкото ако или ако.

Нека да преминем към анализиране на възможните случаи на подреждане на два кръга (фиг. 206).

а) Центровете на окръжностите съвпадат (фиг. 206, а). Такива кръгове се наричат ​​концентрични. Ако радиусите на тези окръжности не са равни, тогава едната от тях лежи вътре в другата. Ако радиусите са равни, те съвпадат.

б) Нека сега центровете на окръжностите са различни. Нека ги свържем с права линия, тя се нарича линия на центровете на дадена двойка окръжности. Относителното положение на кръговете ще зависи само от връзката между стойността на сегмента d, свързващ техните центрове, и стойностите на радиусите на кръговете R, r. Всички възможни значително различни случаи са представени на фиг. 206 (преброяване).

1. Разстоянието между центровете е по-малко от разликата в радиусите:

(Фиг. 206, b), малкият кръг лежи вътре в големия. Това включва и случая на а) съвпадение на центрове (d = 0).

2. Разстоянието между центровете е равно на разликата в радиусите:

(Фиг. 206, s). Малкият кръг лежи вътре в големия, но има една обща точка с него на линията на центровете (казват, че има вътрешно допиране).

3. Разстоянието между центровете е по-голямо от разликата в радиусите, но по-малко от тяхната сума:

(Фиг. 206, d). Всеки кръг лежи отчасти вътре и отчасти извън другия.

Кръговете имат две пресечни точки K и L, разположени симетрично спрямо линията на центровете. Отсечката е обща хорда от две пресичащи се окръжности. Тя е перпендикулярна на линията на центровете.

4. Разстоянието между центровете е равно на сумата от радиусите:

(Фиг. 206, d). Всяка от окръжностите лежи извън другата, но имат обща точка на линията на центровете (външно допиране).

5. Разстоянието между центровете е по-голямо от сумата на радиусите: (фиг. 206, е). Всеки кръг лежи изцяло извън другия. Окръжностите нямат общи точки.

Горната класификация следва напълно от обсъденото. над въпроса за най-голямото и най-малкото разстояние от точка до окръжност. Просто трябва да разгледате две точки на един от кръговете: най-близката и най-отдалечената от центъра на втория кръг. Например, нека разгледаме случая По условие. Но точката на малкия кръг, която е най-отдалечена от O, се намира на разстояние от центъра O. Следователно целият малък кръг лежи вътре в големия кръг. Други случаи се разглеждат по същия начин.

По-специално, ако радиусите на кръговете са равни, тогава са възможни само последните три случая: пресичане, външно допиране, външно местоположение.

Министерство на образованието и науката на Руската федерация

Общинско бюджетно учебно заведение

град Новосибирск "Гимназия № 4"

Секция: математика

ИЗСЛЕДВАНИЯ

по тази тема:

СВОЙСТВА НА ДВА ДОПИРАНИ ОКРУГА

Ученици от 10 клас:

Хазиахметов Радик Илдарович

Зубарев Евгений Владимирович

Ръководител:

Л.Л. Баринова

Учител по математика

Висша квалификационна категория

§ 1. Въведение………..………………………….……………………………………………………3

§ 1.1 Относителното положение на две окръжности………………………………………………………3

§ 2 Имоти и техните доказателства……………………………………………………………………………….....….…4

§ 2.1 Свойство 1……………………………………………………..…………………...….…4

§ 2.2 Свойство 2………………………………………………………………………………………5

§ 2.3 Свойство 3………………………………………………………………………………………6

§ 2.4 Свойство 4………………………………………………………………………………………6

§ 2.5 Свойство 5…………………………………..………………………………………………8

§ 2.6 Свойство 6…………………………………………………………………………………………9

§ 3 Задачи……………………………………………………..…………………………………..…11

Препратки…………………………………………………………………………………….………….13

§ 1. Въведение

Много задачи, включващи две допирателни окръжности, могат да бъдат решени по-кратко и просто чрез познаване на някои от свойствата, които ще бъдат представени по-нататък.

Относителното положение на два кръга

Като начало нека уговорим възможното взаимно положение на двете окръжности. Може да има 4 различни случая.

1. Кръговете не трябва да се пресичат.

2. Пресечете се.

3. Докоснете в една точка от външната страна.

4. Докоснете в една точка вътре.

§ 2. Свойства и техните доказателства

Да преминем директно към доказателството на свойствата.

§ 2.1 Свойство 1

Отсечките между точките на пресичане на допирателните с окръжностите са равни една на друга и равни на два средногеометрични радиуса на дадените окръжности.

Доказателство 1. O 1 A 1 и O 2 B 1 – радиуси, начертани към точките на контакт.

2. О 1 А 1 ┴ А 1 В 1, О2В1 ┴ А 1 В 1 → О 1 А 1 ║ О 2 В 1. (по точка 1)

1. ▲O 1 O 2 D – правоъгълен, т.к О 2 D ┴ О 2 В 1
2. O 1 O 2 = R + r, O 2 D = R – r

1. Според Питагоровата теорема A 1 B 1 = 2√Rr

(O 1 D 2 =(R+r) 2 -(R-r) 2 =R 2 +2Rr+r2-R 2 +2Rr-r 2 =√4Rr=2√Rr)

A 2 B 2 = 2√Rr (доказано по подобен начин)

1) Нека начертаем радиусите в точките на пресичане на допирателните с окръжностите.

2) Тези радиуси ще бъдат перпендикулярни на допирателните и успоредни един на друг.

3) Нека спуснем перпендикуляр от центъра на по-малкия кръг към радиуса на по-големия кръг.

4) Хипотенузата на получения правоъгълен триъгълник е равна на сбора от радиусите на окръжностите. Кракът е равен на тяхната разлика.

5) С помощта на Питагоровата теорема получаваме търсената връзка.

§ 2.2 Свойство 2

Пресечните точки на права линия, която пресича допирателната точка на окръжностите и не лежи в нито една от тях с допирателните, разделят наполовина сегментите на външните допирателни, ограничени от точките на допирателни точки, на части, всяка от които е равно на средното геометрично на радиусите на тези окръжности.

Доказателство 1.Г-ЦА= MA 1 (като допирателни сегменти)

2.MC = MV 1 (като допирателни сегменти)

3.A 1 M = MV 1 = √Rr, A 2 N = NB 2 = √Rr (съгласно точки 1 и 2 )

Изявления, използвани в доказателството Допирателните отсечки, прекарани от една точка към определена окръжност, са равни. Използваме това свойство и за двете дадени окръжности.

§ 2.3 Свойство 3

Дължината на отсечката от вътрешната допирателна, оградена между външните допирателни, е равна на дължината на отсечката от външната допирателна между точките на допир и е равна на два средногеометрични радиуса на дадените окръжности.

Доказателство Това заключение следва от предишното свойство.

MN = MC + CN = 2MC = 2A 1 M = A 1 B 1 = 2√Rr

§ 2.4 Свойство 4

Триъгълникът, образуван от центровете на допирателните окръжности и средата на допирателната отсечка между радиусите, начертани към точките на допир, е правоъгълен. Съотношението на краката му е равно на частното от корените на радиусите на тези окръжности.

Доказателство 1.MO 1 е ъглополовяща на ъгъл A 1 MS, MO 2 е ъглополовяща на ъгъл B 1 MS, т.к. Центърът на окръжност, вписана в ъгъл, лежи върху ъглополовящата на този ъгъл.

2.Съгласно точка 1 РО 1 MS + РСМО 2 = 0,5(РА1МС + РСМВ 1) = 0,5p = p/2

3.РО 1 МО 2 – прав. MC е височината на триъгълника O 1 MO 2, т.к допирателната MN е перпендикулярна на радиусите, прекарани към точките на допир → триъгълниците O 1 MC и MO 2 C са подобни.

4.O 1 M / MO 2 = O 1 C / MC = r / √Rr = √r / R (подобно)

Изявления, използвани в доказателството 1) Центърът на окръжност, вписана в ъгъл, лежи върху ъглополовящата на този ъгъл. Краката на триъгълника са ъглополовящи на ъглите.

2) Използвайки факта, че така образуваните ъгли са равни, намираме, че търсеният ъгъл е прав. Заключаваме, че този триъгълник наистина е правоъгълен.

3) Доказваме подобието на триъгълниците, на които височината (тъй като допирателната е перпендикулярна на радиусите, изтеглени към точките на допиране) разделя правоъгълния триъгълник, и чрез подобие получаваме търсеното съотношение.

§ 2.5 Свойство 5

Триъгълникът, образуван от точката на контакт на окръжностите една с друга и точките на пресичане на окръжностите с допирателната, е правоъгълен. Съотношението на краката му е равно на частното от корените на радиусите на тези окръжности.

Доказателство

1. ▲A 1 MC и ▲SMV 1 са равнобедрени → ÐMA 1 C = ÐMSA 1 = α, ÐMV 1 C = ÐMSV 1 = β.

1. 2α + 2β + RA 1 MC + RSMV 1 = 2p → 2α + 2β = 2p - (RA 1 MC + RSMV 1) = 2p - p = p, α + β = p/2

1. Но RA 1 SV 1 = α + β → RA 1 SV 1 – директно → RA 1 CO 2 = RS 1 O 2 = p/2 – β = α

1. ▲A 1 MC и ▲CO 2 B 1 са подобни → A 1 C / SV 1 = MC / O 2 B 1 = √Rr / R = √r / R

Изявления, използвани в доказателството 1) Записваме сумата от ъглите на триъгълниците, като се възползваме от факта, че те са равнобедрени. Равнобедреността на триъгълниците се доказва с помощта на свойството за равенство на допирателните сегменти.

2) След като сме записали сбора на ъглите по този начин, намираме, че въпросният триъгълник има прав ъгъл, следователно е правоъгълен. Първата част от твърдението е доказана.

3) Използвайки подобието на триъгълниците (за да го обосновем, използваме знака за подобие на два ъгъла) намираме съотношението на катетите на правоъгълен триъгълник.

§ 2.6 Свойство 6

Четириъгълникът, образуван от точките на пресичане на окръжностите с допирателната, е трапец, в който може да се впише окръжност.

Доказателство 1.▲A 1 RA 2 и ▲B 1 PB 2 са равнобедрени, защото A 1 P = RA 2 и B 1 P = PB 2 като допирателни сегменти → ▲A 1 RA 2 и ▲B 1 PB 2 – подобни.

2.A 1 A 2 ║ B 1 B 2, защото съответните ъгли, образувани при пресичането на секанса A 1 B 1, са равни.

1. MN – средна линия според свойство 2 → A 1 A 2 + B 1 B 2 = 2MN = 4√Rr

1. A 1 B 1 + A 2 B 2 = 2√Rr + 2√Rr = 4√Rr = A 1 A 2 + B 1 B 2 → в трапеца A 2 A 1 B 1 B 2 сумата от основите е равна към сбора на страните, а това е необходимо и достатъчно условие за съществуването на вписана окръжност.

Изявления, използвани в доказателството 1) Нека отново използваме свойството на допирателните отсечки. С негова помощ ще докажем равнобедреността на триъгълниците, образувани от пресечната точка на допирателните и допирателните точки.

2) От това ще следва, че тези триъгълници са подобни и техните основи са успоредни. На тази основа заключаваме, че този четириъгълник е трапец.

3) Използвайки свойството (2), което доказахме по-рано, намираме средната линия на трапеца. Той е равен на два средногеометрични радиуса на окръжностите. В получения трапец сборът от основите е равен на сбора от страните, а това е необходимо и достатъчно условие за съществуването на вписана окръжност.

§ 3. Проблеми

Нека да разгледаме практически пример за това как можете да опростите решението на проблем, като използвате свойствата, описани по-горе.

Проблем 1

В триъгълник ABC, страна AC = 15 cm, е вписана окръжност. Втората окръжност докосва първата и страните AB и BC. От страната AB е избрана точка F, а от страната BC е избрана точка M, така че отсечката FM е обща допирателна към окръжностите. Намерете отношението на повърхнините на триъгълник BFM и четириъгълник AFMC, ако FM е 4 cm, а точка M е разположена два пъти по-далече от центъра на едната окръжност, отколкото от центъра на другата.

дадени: FM-обща тангенс AC=15cm FM=4cm O 2 M=2О 1 M

Намерете S BFM /S AFMC

Решение:

1)FM=2√Rr,O 1 M/O 2 M=√r/R

2)2√Rr=4, √r/R=0,5 →r=1,R=4; PQ=FM=4

3)▲BO 1 P и ▲BO 2 Q са подобни → BP/BQ=O 1 P/O 2 Q, BP/(BP+PQ)=r/R,BP/(BP+4)=0,25;BP = 4/3

4)FM+BP=16/3, S FBM =r*P FBM =1*(16/3)=16/3; AC+BQ=15+4/3+4=61/3

5)S ABC =R*P ABC =4*(61/3)=244/3 → S BFM /S AFMC =(16/3):(244/3)=4/61

Проблем 2

В равнобедрен триъгълник ABC са вписани две допирателни окръжности с обща точка D и обща допирателна FK, минаваща през тази точка. Намерете разстоянието между центровете на тези окръжности, ако основата на триъгълника AC = 9 cm, а отсечката от страната на триъгълника, оградена между допирните точки на окръжностите, е 4 cm.

дадени: ABC – равнобедрен триъгълник; FK – обща допирателна на вписани окръжности. AC = 9 cm; NE = 4 см

Решение:

Нека прави AB и CD се пресичат в точка O. Тогава OA = OD, OB = OC, така че CD = = AB = 2√Rr

Точките O 1 и O 2 лежат на ъглополовящата на ъгъл AOD. Симетралата на равнобедрен триъгълник AOD е неговата надморска височина, така че AD ┴ O 1 O 2 и BC ┴ O 1 O 2, което означава

AD ║ BC и ABCD – равнобедрен трапец.

Отсечката MN е неговата средна линия, така че AD + BC = 2MN = 2AB = AB + CD

Следователно в този трапец може да се впише окръжност.

Нека AP е височината на трапеца, правоъгълните триъгълници ARB и O 1 FO 2 са подобни, следователно AP/O 1 F = AB/O 1 O 2 .

От тук намираме това

Библиография

• Приложение към вестник „Първи септември” „Математика” бр.43 2003г.
• Единен държавен изпит 2010. Математика. Задача C4. Гордин Р.К.