Как да повдигнем произведение и частно на степен. Степенуване на произведение и частно

Ако не обърнем внимание на осма степен, какво виждаме тук? Нека да разгледаме програмата за 7 клас. И така, помниш ли? Това е формулата за съкратено умножение, а именно разликата на квадратите! Получаваме:

Внимателно разглеждаме знаменателя. Изглежда много като един от факторите числител, но какво не е наред? Грешен ред на термините. Ако бяха разменени, правилото можеше да се приложи.

Но как да стане това? Оказва се, че е много лесно: тук ни помага четната степен на знаменателя.

Термините магически са разменили местата си. Този "феномен" се отнася за всеки израз в еднаква степен: можем свободно да променяме знаците в скоби.

Но е важно да запомните: всички знаци се променят едновременно!

Да се върнем към примера:

И отново формулата:

цялоназоваваме естествените числа, техните противоположности (т.е. взети със знака "") и числото.

положително цяло число, и не се различава от естествения, тогава всичко изглежда точно както в предишния раздел.

Сега нека да разгледаме новите случаи. Нека започнем с индикатор, равен на.

Всяко число на нулева степен е равно на едно:

Както винаги се питаме: защо е така?

Помислете за мощност с основа. Вземете например и умножете по:

И така, умножихме числото по и получихме същото, както беше -. По какво число трябва да се умножи, за да не се промени нищо? Точно така, на. Средства.

Можем да направим същото с произволно число:

Нека повторим правилото:

Всяко число на нулева степен е равно на едно.

Но има изключения от много правила. И тук също е там - това е число (като основа).

От една страна трябва да е равно на произволна степен - колкото и да умножаваш нулата по себе си, пак получаваш нула, това е ясно. Но от друга страна, като всяко число на нулева степен, то трябва да е равно. И така, каква е истината за това? Математиците решиха да не се намесват и отказаха да повдигнат нулата на нулева степен. Тоест, сега можем не само да разделим на нула, но и да го повдигнем на нулева степен.

Да отидем по-нататък. В допълнение към естествените числа и числата, целите числа включват отрицателни числа. За да разберем какво е отрицателна степен, нека направим същото като миналия път: умножаваме някакво нормално число по същото в отрицателна степен:

От тук вече е лесно да изразите желаното:

Сега разширяваме полученото правило до произволна степен:

И така, нека формулираме правилото:

Число на отрицателна степен е обратното на същото число на положителна степен. Но в същото време базата не може да бъде нула:(защото е невъзможно да се раздели).

Нека обобщим:

I. Изразът не е дефиниран в случай. Ако, тогава.

II. Всяко число на нулева степен е равно на едно: .

III. Число, което не е равно на нула на отрицателна степен, е обратното на същото число на положителна степен: .

Задачи за самостоятелно решаване:

Е, както обикновено, примери за независимо решение:

Анализ на задачите за самостоятелно решаване:

Знам, знам, цифрите са страшни, но на изпита трябва да си готов на всичко! Решете тези примери или анализирайте решението им, ако не сте успели да го решите и ще научите как лесно да се справяте с тях на изпита!

Нека продължим да разширяваме обхвата на числата, "подходящи" като показател.

Сега помислете рационални числа.Кои числа се наричат рационални?

Отговор: всичко, което може да бъде представено като дроб, където и са цели числа, освен това.

За да разберете какво е "дробна степен"Нека разгледаме дроб:

Нека повдигнем двете страни на уравнението на степен:

Сега си спомнете правилото "степен на степен":

Какво число трябва да се повдигне на степен, за да се получи?

Тази формулировка е дефиницията на корена на степен th.

Нека ви напомня: коренът на степен th на число () е число, което, когато е повдигнато на степен, е равно.

Тоест, коренът на та степен е обратната операция на степенуването: .

Оказва се, че. Очевидно този специален случай може да бъде разширен: .

Сега добавете числителя: какво е това? Отговорът е лесен за намиране с правилото мощност към мощност:

Но може ли основата да бъде произволно число? В крайна сметка коренът не може да бъде извлечен от всички числа.

Нито един!

Запомнете правилото: всяко число, повдигнато на четна степен, е положително число. Тоест, невъзможно е да се извлекат корени от четна степен от отрицателни числа!

И това означава, че такива числа не могат да бъдат повдигнати на дробна степен с четен знаменател, тоест изразът няма смисъл.

Какво ще кажете за изразяването?

Но тук възниква проблем.

Числото може да бъде представено като други, намалени дроби, например, или.

И се оказва, че съществува, но не съществува и това са просто два различни записа на едно и също число.

Или друг пример: веднъж, след това можете да го запишете. Но веднага щом напишем индикатора по различен начин, отново имаме проблеми: (тоест получихме напълно различен резултат!).

За да избегнете подобни парадокси, помислете само положителен основен показател с дробен показател.

Така че, ако:

- естествено число;
е цяло число;

Примери:

Степените с рационален показател са много полезни за трансформиране на изрази с корени, например:

5 практически примера

Анализ на 5 примера за обучение

1. Не забравяйте за обичайните свойства на градусите:

2. . Тук си спомняме, че забравихме да научим таблицата на градусите:

все пак - това или. Решението се намира автоматично: .

Е, сега - най-трудното. Сега ще анализираме степен с ирационален показател.

Всички правила и свойства на степените тук са точно същите като за степени с рационален показател, с изключение на

Всъщност по дефиниция ирационалните числа са числа, които не могат да бъдат представени като дроб, където и са цели числа (тоест ирационалните числа са всички реални числа, с изключение на рационалните).

При изучаване на степени с естествен, целочислен и рационален показател, всеки път съставяхме определен „образ“, „аналогия“ или описание с по-познати термини.

Например естествен показател е число, умножено по себе си няколко пъти;

...нулева мощност- това е, така да се каже, число, умножено по себе си веднъж, тоест все още не е започнало да се умножава, което означава, че самото число дори още не се е появило - следователно резултатът е само определена „подготовка на число”, а именно число;

...цяло отрицателно число- сякаш се е случил определен „обратен процес“, тоест числото не е умножено само по себе си, а е разделено.

Между другото, науката често използва степен със сложен експонент, тоест експонентът дори не е реално число.

Но в училище не мислим за подобни трудности; ще имате възможност да разберете тези нови концепции в института.

КЪДЕТО СМЕ СИГУРНИ, ЩЕ ОТИДЕТЕ! (ако се научите да решавате такива примери :))

Например:

Решете сами:

Анализ на решенията:

1. Да започнем с вече обичайното правило за повишаване на степен в степен:

Сега вижте резултата. Той напомня ли ви за нещо? Спомняме си формулата за съкратено умножение на разликата на квадратите:

В такъв случай,

Оказва се, че:

Отговор: .

2. Привеждаме дроби в експоненти в една и съща форма: или десетични, или обикновени. Получаваме например:

Отговор: 16

3. Нищо специално, ние прилагаме обичайните свойства на градусите:

НАПРЕДНАЛО НИВО

Определение за степен

Степента е израз на формата: , където:

— основа на степента;
- експонента.

Степен с естествен показател (n = 1, 2, 3,...)

Повишаването на число на естествена степен n означава умножаване на числото по себе си пъти:

Степен с цяло число (0, ±1, ±2,...)

Ако показателят е положително цяло числономер:

ерекция до нулева мощност:

Изразът е неопределен, защото, от една страна, на произволна степен е това, а от друга страна, всяко число на та степен е това.

Ако показателят е цяло число отрицателнономер:

(защото е невъзможно да се раздели).

Още веднъж за нули: изразът не е дефиниран в случая. Ако, тогава.

Примери:

Степен с рационален показател

- естествено число;
е цяло число;

Примери:

Свойства на степента

За да улесним решаването на проблемите, нека се опитаме да разберем: откъде идват тези свойства? Нека ги докажем.

Да видим: какво е и?

По дефиниция:

И така, от дясната страна на този израз се получава следният продукт:

Но по дефиниция това е степен на число с показател, тоест:

Q.E.D.

Пример : Опростете израза.

Решение : .

Пример : Опростете израза.

Решение : Важно е да се отбележи, че в нашето правило непременнотрябва да има същата основа. Следователно ние комбинираме степените с основата, но оставаме отделен фактор:

Друга важна забележка: това правило - само за произведения на мощности!

При никакви обстоятелства не трябва да пиша това.

Точно както при предишното свойство, нека се обърнем към дефиницията на степента:

Нека го пренаредим така:

Оказва се, че изразът се умножава по себе си веднъж, тоест според дефиницията това е -та степен на числото:

Всъщност това може да се нарече „извеждане на индикатора в скоби“. Но никога не можете да направите това напълно:!

Да си припомним формулите за съкратено умножение: колко пъти искахме да напишем? Но това не е вярно, наистина.

Сила с отрицателна основа.

До този момент сме обсъждали само това, което трябва да бъде индексстепен. Но каква трябва да бъде основата? В градуси от естествено индикатор основата може да бъде произволен брой .

Наистина можем да умножим всяко число едно по друго, независимо дали са положителни, отрицателни или четни. Нека помислим какви знаци ("" или "") ще имат степени на положителни и отрицателни числа?

Например числото ще бъде ли положително или отрицателно? НО? ?

С първото всичко е ясно: без значение колко положителни числа умножаваме едно с друго, резултатът ще бъде положителен.

Но негативните са малко по-интересни. В края на краищата помним едно просто правило от 6-ти клас: „минус по минус дава плюс“. Тоест, или. Но ако умножим по (), получаваме -.

И така до безкрайност: с всяко следващо умножение знакът ще се променя. Възможно е да се формулират такива прости правила:

дористепен, - номер положителен.
Отрицателното число е повишено до странностепен, - номер отрицателен.
Положително число на всяка степен е положително число.
Нула на произволна степен е равна на нула.

Определете сами какъв знак ще имат следните изрази:

1.	2.	3.
4.	5.	6.

успяхте ли Ето и отговорите:

1) ; 2) ; 3) ; 4) ; 5) ; 6) .

В първите четири примера, надявам се всичко е ясно? Просто разглеждаме основата и експонентата и прилагаме съответното правило.

В пример 5) всичко също не е толкова страшно, колкото изглежда: няма значение на какво е равна основата - степента е равна, което означава, че резултатът винаги ще бъде положителен. Е, освен когато основата е нула. Основата не е същата, нали? Очевидно не, тъй като (защото).

Пример 6) вече не е толкова прост. Тук трябва да разберете кое е по-малко: или? Ако си спомним това, става ясно, че, което означава, че основата е по-малка от нула. Тоест прилагаме правило 2: резултатът ще бъде отрицателен.

И отново използваме определението за степен:

Всичко е както обикновено - записваме определението на степените и ги разделяме една на друга, разделяме ги на двойки и получаваме:

Преди да анализираме последното правило, нека решим няколко примера.

Изчислете стойностите на изразите:

Решения :

Получаваме:

Внимателно разглеждаме знаменателя. Изглежда много като един от факторите числител, но какво не е наред? Грешен ред на термините. Ако бяха обърнати, може да се приложи правило 3. Но как да стане това? Оказва се, че е много лесно: тук ни помага четната степен на знаменателя.

Ако го умножите по, нищо не се променя, нали? Но сега изглежда така:

Термините магически са разменили местата си. Този "феномен" се отнася за всеки израз в еднаква степен: можем свободно да променяме знаците в скоби. Но е важно да запомните: всички знаци се променят едновременно!Не може да се замени със смяна само на един неприятен за нас минус!

Да се върнем към примера:

И отново формулата:

И така, последното правило:

Как ще го докажем? Разбира се, както обикновено: нека разширим концепцията за степен и да опростим:

Е, сега нека отворим скобите. Колко букви ще има? пъти по множители - как изглежда? Това не е нищо друго освен определението за операция умножение: общо се оказаха множители. Тоест, по дефиниция това е степен на число с показател:

Пример:

Степен с ирационален показател

Освен информация за степените за средно ниво, ще анализираме степента с ирационален показател. Всички правила и свойства на степените тук са точно същите като за степен с рационален показател, с изключение - в края на краищата, по дефиниция ирационалните числа са числа, които не могат да бъдат представени като дроб, където и са цели числа (т.е. , ирационалните числа са всички реални числа, с изключение на рационалните).

При изучаване на степени с естествен, целочислен и рационален показател, всеки път съставяхме определен „образ“, „аналогия“ или описание с по-познати термини. Например естествен показател е число, умножено по себе си няколко пъти; число до нулева степен е, така да се каже, число, умножено по себе си веднъж, тоест все още не е започнало да се умножава, което означава, че самото число дори още не се е появило - следователно резултатът е само определена „подготовка на число“, а именно число; степен с цяло число отрицателен индикатор - сякаш е настъпил определен „обратен процес“, тоест числото не е умножено само по себе си, а е разделено.

Изключително трудно е да си представим степен с ирационален показател (точно както е трудно да си представим 4-измерно пространство). По-скоро това е чисто математически обект, който математиците са създали, за да разширят концепцията за степен към цялото пространство на числата.

Между другото, науката често използва степен със сложен експонент, тоест експонентът дори не е реално число. Но в училище не мислим за подобни трудности; ще имате възможност да разберете тези нови концепции в института.

Какво правим, ако видим ирационален показател? Опитваме се да се отървем от него! :)

Например:

Решете сами:

Отговори:

Запомнете формулата за разликата на квадратите. Отговор: .
Ние привеждаме дроби в една и съща форма: или двете десетични, или и двете обикновени. Получаваме например: .
Нищо специално, прилагаме обичайните свойства на градусите:

РЕЗЮМЕ НА РАЗДЕЛ И ОСНОВНА ФОРМУЛА

Степенсе нарича израз от формата: , където:

Степен с цяло число

степен, чийто показател е естествено число (т.е. цяло число и положително).

Степен с рационален показател

степен, чийто показател са отрицателни и дробни числа.

Степен с ирационален показател

показател, чийто показател е безкрайна десетична дроб или корен.

Свойства на степента

Характеристики на степените.

Отрицателното число е повишено до дористепен, - номер положителен.
Отрицателното число е повишено до странностепен, - номер отрицателен.
Положително число на всяка степен е положително число.
Нула е равна на всяка степен.
Всяко число на нулева степен е равно.

СЕГА ИМАТЕ ДУМА...

Как ви харесва статията? Кажете ми в коментарите по-долу дали ви харесва или не.

Разкажете ни за опита си с мощността.

Може би имате въпроси. Или предложения.

Пишете в коментарите.

И успех на изпитите!

Моля, имайте предвид, че този раздел се занимава с концепцията градуса само с натурален показатели нула.

Понятието и свойствата на степените с рационални показатели (с отрицателни и дробни) ще бъдат разгледани в уроците за 8 клас.

И така, нека разберем какво е степен на число.За да запишете произведението на число само по себе си, съкратеният запис се използва няколко пъти.

Вместо да умножават шест еднакви множители 4 4 4 4 4 4, те пишат 4 6 и казват „четири на шеста степен“.

4 4 4 4 4 4 = 4 6

Изразът 4 6 се нарича степен на число, където:

4 — основа на степен;
6 — експонент.

По принцип степента с основа "a" и показател "n" се записва с помощта на израза:

Помня!

Степента на числото "а" с естествен показател "n", по-голям от 1, е продуктът "n» Идентични множители, всеки от които е равен на числото "a".

Записът " a n"Чете така:" и на степен n "или" n-та степен на числото a".

Изключение правят записите:

a 2 - може да се произнесе като "а на квадрат";
a 3 - може да се произнесе като "а в куб."

a 2 - "и до втора степен";
a 3 - "a на трета степен."

Специални случаи възникват, ако експонентата е равна на единица или нула (n = 1; n = 0).

Помня!

Степента на числото "a" с експонента n \u003d 1 е самото това число:
a 1 = a

Всяко число на нулева степен е равно на едно.
а 0 = 1

Нула към всяка естествена степен е равна на нула.
0 n = 0

Едно на произволна степен е равно на 1.
1n=1

Израз 0 0 ( от нула до нула мощност) се счита за безсмислено.

(−32) 0 = 1
0 253 = 0
1 4 = 1

Когато решавате примери, трябва да запомните, че повдигането на степен се нарича намиране на числова или буквална стойност след повдигането й на степен.

Пример. Издигане на степен.

5 3 = 5 5 5 = 125
2,5 2 = 2,5 2,5 = 6,25
( · = = 81
256

Степенуване на отрицателно число

Основата на експонентата (числото, което е повдигнато на степен) може да бъде всяко число — положително, отрицателно или нула.

Помня!

Повишаването на положително число на степен води до положително число.

Повишаването на нула до естествена степен води до нула.

Когато повдигате отрицателно число на степен, резултатът може да бъде или положително число, или отрицателно число. Зависи дали показателят е четно или нечетно число.

Разгледайте примери за повдигане на отрицателни числа на степен.

От разгледаните примери се вижда, че ако отрицателно число се повдигне на нечетна степен, тогава се получава отрицателно число. Тъй като произведението на нечетен брой отрицателни фактори е отрицателно.

Ако отрицателно число се повдигне на четна степен, тогава се получава положително число. Тъй като произведението на четен брой отрицателни фактори е положително.

Помня!

Отрицателно число, повишено на четна степен, е положително число.

Отрицателно число, повишено на нечетна степен, е отрицателно число.

Квадратът на всяко число е положително число или нула, тоест:

a 2 ≥ 0 за всяко a .

2 (−3) 2 = 2 (−3) (−3) = 2 9 = 18
−5 (−2) 3 = −5 (−8) = 40

Забележка!

При решаването на примери за степенуване често се допускат грешки, забравяйки, че записите (−5) 4 и −5 4 са различни изрази. Резултатите от повдигането на степен на тези изрази ще бъдат различни.

Изчислете (−5) 4 означава да намерите стойността на четвъртата степен на отрицателно число.

(−5) 4 = (−5) (−5) (−5) (−5) = 625

Докато намирането на "-5 4" означава, че примерът трябва да бъде решен в 2 стъпки:

Повишете положителното число 5 на четвърта степен.
5 4 = 5 5 5 5 = 625
Поставете знак минус пред получения резултат (т.е. извършете действие за изваждане).
−5 4 = −625

Пример. Изчислете: −6 2 − (−1) 4

−6 2 − (−1) 4 = −37

6 2 = 6 6 = 36
−6 2 = −36
(−1) 4 = (−1) (−1) (−1) (−1) = 1
−(−1) 4 = −1
−36 − 1 = −37

Процедура за примери със степени

Изчисляването на стойност се нарича действие на степенуване. Това е трето етапно действие.

Помня!

В изрази със степени, които не съдържат скоби, първо изпълнете степенуване, тогава умножение и деление, и в края събиране и изваждане.

Ако в израза има скоби, тогава първо в реда, посочен по-горе, се изпълняват действията в скобите, а след това останалите действия в същия ред отляво надясно.

Пример. Изчисли:

За да улесните решаването на примери, е полезно да знаете и използвате градусната таблица, която можете да изтеглите безплатно на нашия уебсайт.

За да проверите резултатите си, можете да използвате калкулатора на нашия уебсайт "

Разбрахме каква е степента на число като цяло. Сега трябва да разберем как да го изчислим правилно, т.е. повишаване на числата до степени. В този материал ще анализираме основните правила за изчисляване на степента в случай на цяло число, естествен, дробен, рационален и ирационален показател. Всички определения ще бъдат илюстрирани с примери.

Концепцията за степенуване

Нека започнем с формулирането на основните определения.

Определение 1

степенуванее изчисляването на стойността на степента на някакво число.

Тоест думите "изчисляване на стойността на степента" и "постепенно" означават едно и също нещо. Така че, ако задачата е „Повишете числото 0 , 5 на пета степен“, това трябва да се разбира като „изчислете стойността на степента (0 , 5) 5 .

Сега даваме основните правила, които трябва да се спазват при такива изчисления.

Припомнете си какво е степен на число с естествен показател. За степен с основа а и показател n, това ще бъде произведението на n-тия брой множители, всеки от които е равен на а. Това може да се напише така:

За да изчислите стойността на степента, трябва да извършите операцията на умножение, тоест да умножите основите на степента посочения брой пъти. Самата концепция за степен с естествен показател се основава на способността за бързо умножаване. Да дадем примери.

Пример 1

Условие: Повишете - 2 на степен 4 .

Решение

Използвайки дефиницията по-горе, записваме: (− 2) 4 = (− 2) (− 2) (− 2) (− 2) . След това просто трябва да следваме тези стъпки и да получим 16 .

Да вземем един по-сложен пример.

Пример 2

Изчислете стойността 3 2 7 2

Решение

Този запис може да се пренапише като 3 2 7 · 3 2 7 . По-рано разгледахме как да умножим правилно смесените числа, споменати в условието.

Изпълнете тези стъпки и получете отговора: 3 2 7 3 2 7 = 23 7 23 7 = 529 49 = 10 39 49

Ако задачата показва необходимостта от повдигане на ирационални числа на естествена степен, ще трябва първо да закръглим основите им до цифра, която ще ни позволи да получим отговор с желаната точност. Да вземем пример.

Пример 3

Извършете повдигане на квадрат на числото π.

Решение

Нека първо го закръглим до стотни. Тогава π 2 ≈ (3, 14) 2 = 9, 8596. Ако π ≈ 3 . 14159, тогава ще получим по-точен резултат: π 2 ≈ (3, 14159) 2 = 9, 8695877281.

Имайте предвид, че необходимостта от изчисляване на степените на ирационални числа на практика възниква сравнително рядко. След това можем да запишем отговора като самата степен (ln 6) 3 или да преобразуваме, ако е възможно: 5 7 = 125 5 .

Отделно трябва да се посочи каква е първата степен на числото. Тук можете просто да запомните, че всяко число, повдигнато на първа степен, ще остане себе си:

Това става ясно от протокола. .

Не зависи от основата на степента.

Пример 4

И така, (− 9) 1 = − 9 и 7 3, повдигнато на първа степен, остава равно на 7 3 .

За удобство ще анализираме три случая поотделно: ако показателят е положително цяло число, ако е нула и ако е отрицателно цяло число.

В първия случай това е същото като повдигане на естествена степен: в края на краищата положителните цели числа принадлежат към набора от естествени числа. Вече описахме как да работим с такива степени по-горе.

Сега нека видим как правилно да вдигнем до нулева мощност. При основа, която е различна от нула, това изчисление винаги дава резултат от 1 . По-рано обяснихме, че 0-та степен на a може да бъде дефинирана за всяко реално число, което не е равно на 0, и a 0 = 1.

Пример 5

5 0 = 1 , (- 2 , 56) 0 = 1 2 3 0 = 1

0 0 - не е определено.

Остава ни само случай на степен с отрицателен цяло число. Вече обсъдихме, че такива степени могат да бъдат записани като дроб 1 a z, където a е произволно число, а z е отрицателно цяло число. Виждаме, че знаменателят на тази дроб не е нищо повече от обикновена степен с положително цяло число и вече сме се научили как да го изчисляваме. Нека дадем примери за задачи.

Пример 6

Повишете 2 на степен -3.

Решение

Използвайки дефиницията по-горе, записваме: 2 - 3 = 1 2 3

Изчисляваме знаменателя на тази дроб и получаваме 8: 2 3 \u003d 2 2 2 \u003d 8.

Тогава отговорът е: 2 - 3 = 1 2 3 = 1 8

Пример 7

Повишете 1, 43 на степен -2.

Решение

Преформулирайте: 1 , 43 - 2 = 1 (1 , 43) 2

Изчисляваме квадрата в знаменателя: 1,43 1,43. Десетичните числа могат да се умножат по следния начин: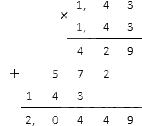

В резултат на това получихме (1, 43) - 2 = 1 (1, 43) 2 = 1 2 , 0449 . Остава да напишем този резултат под формата на обикновена фракция, за която е необходимо да я умножим по 10 хиляди (вижте материала за преобразуване на дроби).

Отговор: (1, 43) - 2 = 10000 20449

Отделен случай е повишаване на число на минус първа степен. Стойността на такава степен е равна на числото, противоположно на първоначалната стойност на основата: a - 1 \u003d 1 a 1 \u003d 1 a.

Пример 8

Пример: 3 − 1 = 1/3

9 13 - 1 = 13 9 6 4 - 1 = 1 6 4 .

Как да повдигнем число на дробна степен

За да извършим такава операция, трябва да си припомним основната дефиниция на степен с дробен показател: a m n \u003d a m n за всяко положително a, цяло число m и естествено n.

Определение 2

По този начин изчисляването на дробна степен трябва да се извърши на две стъпки: повишаване на степен на цяло число и намиране на корена на n-та степен.

Имаме равенството a m n = a m n , което, като се имат предвид свойствата на корените, обикновено се използва за решаване на задачи във формата a m n = a n m . Това означава, че ако повдигнем числото a на дробна степен m / n, тогава първо извличаме корена на n-та степен от a, след което повдигаме резултата на степен с цяло число m.

Нека илюстрираме с пример.

Пример 9

Пресметнете 8 - 2 3 .

Решение

Метод 1. Съгласно основната дефиниция можем да представим това като: 8 - 2 3 \u003d 8 - 2 3

Сега нека изчислим степента под корена и извлечем третия корен от резултата: 8 - 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4

Метод 2. Нека преобразуваме основното равенство: 8 - 2 3 \u003d 8 - 2 3 \u003d 8 3 - 2

След това изваждаме корена 8 3 - 2 = 2 3 3 - 2 = 2 - 2 и повдигаме резултата на квадрат: 2 - 2 = 1 2 2 = 1 4

Виждаме, че решенията са идентични. Можете да използвате какъвто начин желаете.

Има случаи, когато степента има показател, изразен като смесено число или десетична дроб. За по-лесно изчисление е по-добре да го замените с обикновена дроб и да броите, както е посочено по-горе.

Пример 10

Повдигнете 44,89 на степен 2,5.

Решение

Нека преобразуваме стойността на индикатора в обикновена дроб: 44 , 89 2 , 5 = 44 , 89 5 2 .

И сега изпълняваме всички действия, посочени по-горе в ред: 44 , 89 5 2 = 44 , 89 5 = 44 , 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = = 1350125107 100000 = 13 501, 25107

Отговор: 13501, 25107.

Ако има големи числа в числителя и знаменателя на дробен показател, тогава изчисляването на такива показатели с рационални показатели е доста трудна работа. Обикновено изисква компютърна технология.

Отделно се спираме на степента с нулева основа и дробен показател. На израз от формата 0 m n може да се придаде следното значение: ако m n > 0, тогава 0 m n = 0 m n = 0 ; ако m n< 0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0 7 12 = 0 , 0 3 2 5 = 0 , 0 0 , 024 = 0 , а в целую отрицательную - значения не имеет: 0 - 4 3 .

Как да повдигнем число на ирационална степен

Необходимостта от изчисляване на стойността на степента, в индикатора на която има ирационално число, не възниква толкова често. На практика задачата обикновено се ограничава до изчисляване на приблизителна стойност (до определен брой десетични знаци). Това обикновено се изчислява на компютър поради сложността на такива изчисления, така че няма да се спираме на това подробно, ще посочим само основните разпоредби.

Ако трябва да изчислим стойността на степента a с ирационален показател a , тогава вземаме десетичното приближение на показателя и броим от него. Резултатът ще бъде приблизителен отговор. Колкото по-точно е взетото десетично приближение, толкова по-точен е отговорът. Нека покажем с пример:

Пример 11

Изчислете приблизителната стойност на 2 на степен 1,174367....

Решение

Ограничаваме се до десетичната апроксимация a n = 1, 17. Нека направим изчисленията, използвайки това число: 2 1 , 17 ≈ 2 , 250116 . Ако вземем, например, приближението a n = 1 , 1743 , тогава отговорът ще бъде малко по-точен: 2 1 , 174367 . . . ≈ 2 1. 1743 ≈ 2 .256833 .

Ако забележите грешка в текста, моля, маркирайте я и натиснете Ctrl+Enter

Напомняме ви, че в този урок разбираме степенни свойствас натурални показатели и нула. Степените с рационални показатели и техните свойства ще бъдат разгледани в уроците за 8 клас.

Експонента с естествен показател има няколко важни свойства, които ви позволяват да опростите изчисленията в примери за степен.

Имот #1
Продукт на мощности

Помня!

При умножаване на степени с една и съща основа, основата остава непроменена, а показателите се добавят.

a m a n \u003d a m + n, където " a"- всяко число и" m", " n"- всякакви естествени числа.

Това свойство на степените също засяга произведението на три или повече степени.

Опростете израза.
b b 2 b 3 b 4 b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
Присъства като степен.
6 15 36 = 6 15 6 2 = 6 15 6 2 = 6 17
Присъства като степен.
(0,8) 3 (0,8) 12 = (0,8) 3 + 12 = (0,8) 15

важно!

Моля, обърнете внимание, че в посоченото свойство става дума само за умножаване на степени с същите основания . Не се отнася за добавянето им.

Не можете да замените сбора (3 3 + 3 2) с 3 5 . Това е разбираемо, ако
пресметнете (3 3 + 3 2) = (27 + 9) = 36 и 3 5 = 243

Имот №2
Частни степени

Помня!

При деление на степени с една и съща основа основата остава непроменена и показателят на делителя се изважда от показателя на делителя.

= 11 3 − 2 4 2 − 1 = 11 4 = 44

Пример. Решете уравнението. Използваме свойството на частичните степени.
3 8: t = 3 4

T = 3 8 − 4

Отговор: t = 3 4 = 81

Използвайки свойства № 1 и № 2, можете лесно да опростявате изрази и да извършвате изчисления.

Пример. Опростете израза.
4 5m + 6 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
Пример. Намерете стойността на израз, като използвате свойствата на степента.
= = = 2 9 + 2
2 5
= 2 11
2 5
= 2 11 − 5 = 2 6 = 64
важно!
Моля, обърнете внимание, че свойство 2 се занимава само с разделението на правомощията със същите основи.

Не можете да замените разликата (4 3 −4 2) с 4 1 . Това е разбираемо, ако вземем предвид (4 3 −4 2) = (64 − 16) = 48 и 4 1 = 4

Бъди внимателен!

Имот #3
степенуване

Помня!
При повишаване на степен на степен основата на степента остава непроменена, а показателите се умножават.
(a n) m \u003d a n m, където "a" е произволно число, а "m", "n" са произволни естествени числа.

Свойства 4
Продуктова степен

Помня!
При повдигане на продукт на степен, всеки от факторите се повдига на степен. След това резултатите се умножават.
(a b) n \u003d a n b n, където "a", "b" са произволни рационални числа; "n" - всяко естествено число.
- Пример 1
  (6 a 2 b 3 c) 2 = 6 2 a 2 2 b 3 2 s 1 2 = 36 a 4 b 6 s 2
- Пример 2
  (−x 2 y) 6 = ((−1) 6 x 2 6 y 1 6) = x 12 y 6
важно!
Моля, обърнете внимание, че свойство № 4, подобно на други свойства на степените, също се прилага в обратен ред.
(a n b n)= (a b) n
Тоест, за да умножите степени с еднакви показатели, можете да умножите основите и да оставите степента непроменена.
- Пример. Изчисли.
  2 4 5 4 = (2 5) 4 = 10 4 = 10 000
- Пример. Изчисли.
  0,5 16 2 16 = (0,5 2) 16 = 1
В по-сложни примери може да има случаи, когато умножението и делението трябва да се извършват на степени с различни основи и различни степени. В този случай ви съветваме да направите следното.

Например, 4 5 3 2 = 4 3 4 2 3 2 = 4 3 (4 3) 2 = 64 12 2 = 64 144 = 9216

Пример за степенуване на десетична дроб.
4 21 (−0,25) 20 = 4 4 20 (−0,25) 20 = 4 (4 (−0,25)) 20 = 4 (−1) 20 = 4 1 = четири
Свойства 5
Степен на частното (дроби)

Помня!
За да повдигнете частно на степен, можете да повдигнете дивидента и делителя поотделно на тази степен и да разделите първия резултат на втория.
(a: b) n \u003d a n: b n, където "a", "b" са произволни рационални числа, b ≠ 0, n е всяко естествено число.
- Пример. Изразете израза като частични степени.
  (5: 3) 12 = 5 12: 3 12
Напомняме ви, че частното може да бъде представено като дроб. Затова ще се спрем по-подробно на темата за повдигане на дроб на степен на следващата страница.

основна цел

Да запознае учениците със свойствата на степените с естествени показатели и да ги научи да извършват действия със степени.

Тема „Степен и нейните свойства“включва три въпроса:

Определяне на градуса с натурален показател.
Умножение и деление на степени.
Степенуване на произведение и степен.

тестови въпроси

Формулирайте дефиницията на степен с естествен показател по-голям от 1. Дайте пример.
Формулирайте дефиниция на степента с показател 1. Дайте пример.
Какъв е редът на операциите при изчисляване на стойността на израз, съдържащ степени?
Формулирайте основното свойство на степента. Дай пример.
Формулирайте правило за умножение на степени с една и съща основа. Дай пример.
Формулирайте правило за деление на степени с еднакви основи. Дай пример.
Формулирайте правилото за степенуване на продукт. Дай пример. Докажете тъждеството (ab) n = a n b n .
Формулирайте правило за повишаване на степен на степен. Дай пример. Докажете идентичността (a m) n = a m n .

Определение за степен.

степен на числото ас естествен показател н, по-голямо от 1, се нарича произведение от n фактора, всеки от които е равен на а. степен на числото асъс степен 1 се нарича самото число а.

Степен с основа аи индикатор не написано така: a n. Той гласи " адо степента н”; “ n-та степен на число а ”.

По дефиниция на степен:

a 4 = a a a a

. . . . . . . . . . . .

Намирането на стойността на степента се нарича степенуване .

1. Примери за степенуване:

3 3 = 3 3 3 = 27

0 4 = 0 0 0 0 = 0

(-5) 3 = (-5) (-5) (-5) = -125

25 ; 0,09 ;

25 = 5 2 ; 0,09 = (0,3) 2 ; .

27 ; 0,001 ; 8 .

27 = 3 3 ; 0,001 = (0,1) 3 ; 8 = 2 3 .

4. Намерете стойностите на израза:

а) 3 10 3 = 3 10 10 10 = 3 1000 = 3000

б) -2 4 + (-3) 2 = 7
2 4 = 16
(-3) 2 = 9
-16 + 9 = 7

Опция 1

а) 0,3 0,3 0,3

в) b b b b b b b

г) (-x) (-x) (-x) (-x)

д) (ab) (ab) (ab)

2. Повдигнете на квадрат числата:

3. Кубирайте числата:

4. Намерете стойностите на израза:

в) -1 4 + (-2) 3

г) -4 3 + (-3) 2

д) 100 - 5 2 4

Умножение на степени.

За всяко число a и произволни числа m и n е вярно следното:

a m a n = a m + n.

Доказателство:

правило : При умножаване на степени с една и съща основа, основите остават същите, а показателите се добавят.

a m a n a k = a m + n a k = a (m + n) + k = a m + n + k

а) x 5 x 4 = x 5 + 4 = x 9

б) y y 6 = y 1 y 6 = y 1 + 6 = y 7

в) b 2 b 5 b 4 \u003d b 2 + 5 + 4 \u003d b 11

г) 3 4 9 = 3 4 3 2 = 3 6

д) 0,01 0,1 3 = 0,1 2 0,1 3 = 0,1 5

а) 2 3 2 = 2 4 = 16

б) 3 2 3 5 = 3 7 = 2187

Опция 1

1. Представяне като степен:

а) x 3 x 4 д) x 2 x 3 x 4

б) a 6 a 2 g) 3 3 9

в) y 4 y h) 7 4 49

г) а а 8 и) 16 2 7

д) 2 3 2 4 к) 0,3 3 0,09

2. Представете като степен и намерете стойността в таблицата:

а) 2 2 2 3 в) 8 2 5

б) 3 4 3 2 г) 27 243

Деление на степени.

За всяко число a0 и произволни естествени числа m и n, такива че m>n, е валидно следното:

a m: a n = a m - n

Доказателство:

a m - n a n = a (m - n) + n = a m - n + n = a m

по дефиниция за частно:

a m: a n \u003d a m - n.

правило: При деление на степени с една и съща основа, основата остава същата и показателят на делителя се изважда от степента на делителя.

определение: Степента на ненулево число с нулев показател е равна на единица:

защото a n: a n = 1 за a0.

а) x 4: x 2 \u003d x 4 - 2 \u003d x 2

б) y 8: y 3 = y 8 - 3 = y 5

в) a 7: a \u003d a 7: a 1 \u003d a 7 - 1 = a 6

d) s 5:s 0 = s 5:1 = s 5

а) 5 7:5 5 = 5 2 = 25

б) 10 20:10 17 = 10 3 = 1000

в)

G)

д)

Опция 1

1. Изразете частното като степен:

2. Намерете стойностите на изразите:

Издигане на степен на продукт.

За всякакви a и b и произволно естествено число n:

(ab) n = a n b n

Доказателство:

По определение на степен

(ab) n =

Групирайки факторите a и факторите b поотделно, получаваме:

Доказаното свойство на степента на произведението се простира до степента на произведението на три или повече фактора.

Например:

(a b c) n = a n b n c n;

(a b c d) n = a n b n c n d n.

правило: При повдигане на продукт на степен, всеки фактор се повдига на тази степен и резултатът се умножава.

1. Повдигнете на степен:

a) (a b) 4 = a 4 b 4

б) (2 x y) 3 \u003d 2 3 x 3 y 3 \u003d 8 x 3 y 3

в) (3 а) 4 = 3 4 а 4 = 81 а 4

г) (-5 y) 3 \u003d (-5) 3 y 3 \u003d -125 y 3

д) (-0,2 x y) 2 \u003d (-0,2) 2 x 2 y 2 \u003d 0,04 x 2 y 2

f) (-3 a b c) 4 = (-3) 4 a 4 b 4 c 4 = 81 a 4 b 4 c 4

2. Намерете стойността на израза:

а) (2 10) 4 = 2 4 10 4 = 16 1000 = 16 000

б) (3 5 20) 2 = 3 2 100 2 = 9 10 000 = 90 000

в) 2 4 5 4 = (2 5) 4 = 10 4 = 10000

г) 0,25 11 4 11 = (0,25 4) 11 = 1 11 = 1

д)

Опция 1

1. Повдигнете на степен:

б) (2 а в) 4

д) (-0,1 х у) 3

2. Намерете стойността на израза:

б) (5 7 20) 2

степенуване.

За всяко число a и произволни естествени числа m и n:

(a m) n = a m n

Доказателство:

По определение на степен

(a m) n =

правило: При повишаване на степен на степен, основата се оставя същата, а показателите се умножават.

1. Повдигнете на степен:

(a 3) 2 = a 6 (x 5) 4 = x 20

(y 5) 2 = y 10 (b 3) 3 = b 9

2. Опростете изразите:

а) a 3 (a 2) 5 = a 3 a 10 = a 13

b) (b 3) 2 b 7 \u003d b 6 b 7 \u003d b 13

в) (x 3) 2 (x 2) 4 \u003d x 6 x 8 \u003d x 14

г) (y y 7) 3 = (y 8) 3 = y 24