Πώς να αυξήσετε ένα προϊόν και ένα πηλίκο σε μια ισχύ. Εκτίμηση προϊόντος και πηλίκου

Αν δεν προσέξουμε τον όγδοο βαθμό, τι βλέπουμε εδώ; Ας ρίξουμε μια ματιά στο πρόγραμμα της 7ης τάξης. Λοιπόν, θυμάσαι; Αυτός είναι ο συντομευμένος τύπος πολλαπλασιασμού, δηλαδή η διαφορά των τετραγώνων! Παίρνουμε:

Εξετάζουμε προσεκτικά τον παρονομαστή. Μοιάζει πολύ με έναν από τους αριθμητικούς παράγοντες, αλλά τι φταίει; Λανθασμένη σειρά όρων. Εάν ανταλλάσσονταν, θα μπορούσε να ισχύει ο κανόνας.

Αλλά πώς να το κάνουμε αυτό; Αποδεικνύεται ότι είναι πολύ εύκολο: ο άρτιος βαθμός του παρονομαστή μας βοηθά εδώ.

Οι όροι έχουν αλλάξει τόπους ως δια μαγείας. Αυτό το «φαινόμενο» ισχύει για οποιαδήποτε έκφραση σε άρτιο βαθμό: μπορούμε ελεύθερα να αλλάξουμε τα σημάδια σε αγκύλες.

Αλλά είναι σημαντικό να θυμάστε: όλα τα σημάδια αλλάζουν ταυτόχρονα!

Ας επιστρέψουμε στο παράδειγμα:

Και πάλι ο τύπος:

ολόκληροςονομάζουμε τους φυσικούς αριθμούς, τα αντίθετά τους (δηλαδή λαμβάνονται με το πρόσημο «») και τον αριθμό.

θετικός ακέραιος, και δεν διαφέρει από το φυσικό, τότε όλα μοιάζουν ακριβώς όπως στην προηγούμενη ενότητα.

Ας δούμε τώρα νέες περιπτώσεις. Ας ξεκινήσουμε με έναν δείκτη ίσο με.

Οποιοσδήποτε αριθμός στη μηδενική ισχύ είναι ίσος με ένα:

Όπως πάντα, αναρωτιόμαστε: γιατί συμβαίνει αυτό;

Σκεφτείτε λίγη δύναμη με βάση. Πάρτε, για παράδειγμα, και πολλαπλασιάστε με:

Έτσι, πολλαπλασιάσαμε τον αριθμό επί, και πήραμε τον ίδιο όπως ήταν -. Με ποιον αριθμό πρέπει να πολλαπλασιαστεί για να μην αλλάξει τίποτα; Αυτό είναι σωστό, επάνω. Που σημαίνει.

Μπορούμε να κάνουμε το ίδιο με έναν αυθαίρετο αριθμό:

Ας επαναλάβουμε τον κανόνα:

Οποιοσδήποτε αριθμός στη μηδενική ισχύ είναι ίσος με ένα.

Υπάρχουν όμως εξαιρέσεις σε πολλούς κανόνες. Και εδώ είναι επίσης εκεί - αυτός είναι ένας αριθμός (ως βάση).

Από τη μια πλευρά, πρέπει να είναι ίσο με οποιοδήποτε βαθμό - όσο κι αν πολλαπλασιάσετε το μηδέν με τον εαυτό του, εξακολουθείτε να παίρνετε μηδέν, αυτό είναι ξεκάθαρο. Αλλά από την άλλη πλευρά, όπως κάθε αριθμός στον μηδενικό βαθμό, πρέπει να είναι ίσος. Ποια είναι λοιπόν η αλήθεια αυτού; Οι μαθηματικοί αποφάσισαν να μην εμπλακούν και αρνήθηκαν να ανεβάσουν το μηδέν στη μηδενική ισχύ. Δηλαδή, τώρα μπορούμε όχι μόνο να διαιρέσουμε με το μηδέν, αλλά και να το ανεβάσουμε στη μηδενική ισχύ.

Ας πάμε παρακάτω. Εκτός από τους φυσικούς αριθμούς και τους αριθμούς, οι ακέραιοι περιλαμβάνουν αρνητικούς αριθμούς. Για να καταλάβουμε τι είναι αρνητικός βαθμός, ας κάνουμε το ίδιο με την προηγούμενη φορά: πολλαπλασιάζουμε κάποιον κανονικό αριθμό με τον ίδιο σε αρνητικό βαθμό:

Από εδώ είναι ήδη εύκολο να εκφράσουμε το επιθυμητό:

Τώρα επεκτείνουμε τον κανόνα που προκύπτει σε αυθαίρετο βαθμό:

Ας διαμορφώσουμε λοιπόν τον κανόνα:

Ένας αριθμός σε μια αρνητική δύναμη είναι το αντίστροφο του ίδιου αριθμού σε μια θετική δύναμη. Αλλα ΤΑΥΤΟΧΡΟΝΑ Η βάση δεν μπορεί να είναι μηδενική:(γιατί είναι αδύνατο να διαιρεθεί).

Ας συνοψίσουμε:

I. Η έκφραση δεν ορίζεται σε περίπτωση. Αν τότε.

II. Οποιοσδήποτε αριθμός στη μηδενική ισχύ ισούται με ένα: .

III. Ένας αριθμός που δεν είναι ίσος με το μηδέν σε μια αρνητική δύναμη είναι το αντίστροφο του ίδιου αριθμού σε μια θετική δύναμη: .

Εργασίες για ανεξάρτητη λύση:

Λοιπόν, ως συνήθως, παραδείγματα για μια ανεξάρτητη λύση:

Ανάλυση εργασιών για ανεξάρτητη λύση:

Ξέρω, ξέρω, τα νούμερα είναι τρομακτικά, αλλά στις εξετάσεις πρέπει να είσαι έτοιμος για όλα! Λύστε αυτά τα παραδείγματα ή αναλύστε τη λύση τους αν δεν μπορούσατε να τη λύσετε και θα μάθετε πώς να τα αντιμετωπίζετε εύκολα στις εξετάσεις!

Ας συνεχίσουμε να επεκτείνουμε το εύρος των αριθμών "κατάλληλων" ως εκθέτης.

Τώρα σκεφτείτε ρητοί αριθμοί.Ποιοι αριθμοί ονομάζονται ρητικοί;

Απάντηση: όλα όσα μπορούν να αναπαρασταθούν ως κλάσμα, όπου και είναι ακέραιοι, επιπλέον.

Για να καταλάβουμε τι είναι "κλασματικός βαθμός"Ας εξετάσουμε ένα κλάσμα:

Ας υψώσουμε και τις δύο πλευρές της εξίσωσης σε δύναμη:

Τώρα θυμηθείτε τον κανόνα "πτυχίο σε πτυχίο":

Ποιος αριθμός πρέπει να αυξηθεί σε μια δύναμη για να ληφθεί;

Αυτή η διατύπωση είναι ο ορισμός της ρίζας του ου βαθμού.

Να σας υπενθυμίσω: η ρίζα της ης δύναμης ενός αριθμού () είναι ένας αριθμός που, όταν αυξάνεται σε δύναμη, είναι ίσος.

Δηλαδή, η ρίζα του ου βαθμού είναι η αντίστροφη πράξη της εκθέσεως: .

Τελικά φαίνεται πως. Προφανώς, αυτή η ειδική περίπτωση μπορεί να επεκταθεί: .

Τώρα προσθέστε τον αριθμητή: τι είναι; Η απάντηση είναι εύκολο να ληφθεί με τον κανόνα power-to-power:

Μπορεί όμως η βάση να είναι οποιοσδήποτε αριθμός; Εξάλλου, η ρίζα δεν μπορεί να εξαχθεί από όλους τους αριθμούς.

Κανένας!

Θυμηθείτε τον κανόνα: οποιοσδήποτε αριθμός ανυψωθεί σε άρτια δύναμη είναι θετικός αριθμός. Δηλαδή, είναι αδύνατο να εξαχθούν ρίζες ζυγού βαθμού από αρνητικούς αριθμούς!

Και αυτό σημαίνει ότι τέτοιοι αριθμοί δεν μπορούν να αυξηθούν σε κλασματική ισχύ με άρτιο παρονομαστή, δηλαδή η έκφραση δεν έχει νόημα.

Τι γίνεται με την έκφραση;

Εδώ όμως προκύπτει ένα πρόβλημα.

Ο αριθμός μπορεί να αναπαρασταθεί ως άλλα, μειωμένα κλάσματα, για παράδειγμα, ή.

Και αποδεικνύεται ότι υπάρχει, αλλά δεν υπάρχει, και πρόκειται μόνο για δύο διαφορετικές εγγραφές του ίδιου αριθμού.

Ή ένα άλλο παράδειγμα: μία φορά, τότε μπορείτε να το γράψετε. Μόλις όμως γράψουμε τον δείκτη με διαφορετικό τρόπο, ξαναμπαίνουμε σε μπελάδες: (δηλαδή, πήραμε ένα τελείως διαφορετικό αποτέλεσμα!).

Για να αποφύγετε τέτοια παράδοξα, σκεφτείτε μόνο θετικός εκθέτης βάσης με κλασματικό εκθέτη.

Οπότε αν:

- φυσικός αριθμός;
είναι ακέραιος αριθμός?

Παραδείγματα:

Οι δυνάμεις με λογικό εκθέτη είναι πολύ χρήσιμες για τον μετασχηματισμό εκφράσεων με ρίζες, για παράδειγμα:

5 παραδείγματα πρακτικής

Ανάλυση 5 παραδειγμάτων για εκπαίδευση

1. Μην ξεχνάτε τις συνήθεις ιδιότητες των βαθμών:

2. . Εδώ θυμίζουμε ότι ξεχάσαμε να μάθουμε τον πίνακα πτυχίων:

μετά από όλα - αυτό ή. Η λύση βρίσκεται αυτόματα: .

Λοιπόν, τώρα - το πιο δύσκολο. Τώρα θα αναλύσουμε βαθμό με παράλογο εκθέτη.

Όλοι οι κανόνες και οι ιδιότητες των μοιρών εδώ είναι ακριβώς οι ίδιοι όπως για τους βαθμούς με λογικό εκθέτη, με εξαίρεση

Πράγματι, εξ ορισμού, οι παράλογοι αριθμοί είναι αριθμοί που δεν μπορούν να αναπαρασταθούν ως κλάσμα, όπου και είναι ακέραιοι (δηλαδή, οι άρρητοι αριθμοί είναι όλοι πραγματικοί αριθμοί εκτός από τους ρητούς).

Όταν μελετάμε πτυχία με φυσικό, ακέραιο και ορθολογικό δείκτη, κάθε φορά φτιάχναμε μια συγκεκριμένη «εικόνα», «αναλογία» ή περιγραφή με πιο οικείους όρους.

Για παράδειγμα, ένας φυσικός εκθέτης είναι ένας αριθμός πολλαπλασιασμένος από τον εαυτό του πολλές φορές.

...μηδενική ισχύς- αυτός είναι, σαν να λέγαμε, ένας αριθμός πολλαπλασιασμένος από τον εαυτό του μία φορά, δηλαδή, δεν έχει αρχίσει ακόμη να πολλαπλασιάζεται, πράγμα που σημαίνει ότι ο ίδιος ο αριθμός δεν έχει καν εμφανιστεί ακόμα - επομένως, το αποτέλεσμα είναι μόνο μια ορισμένη «προετοιμασία έναν αριθμό», δηλαδή έναν αριθμό·

...αρνητικός ακέραιος εκθέτης- είναι σαν να έχει λάβει χώρα μια συγκεκριμένη «αντίστροφη διαδικασία», δηλαδή ο αριθμός δεν πολλαπλασιάστηκε από μόνος του, αλλά διαιρέθηκε.

Παρεμπιπτόντως, η επιστήμη χρησιμοποιεί συχνά έναν βαθμό με σύνθετο εκθέτη, δηλαδή, ένας εκθέτης δεν είναι καν πραγματικός αριθμός.

Αλλά στο σχολείο, δεν σκεφτόμαστε τέτοιες δυσκολίες· θα έχετε την ευκαιρία να κατανοήσετε αυτές τις νέες έννοιες στο ινστιτούτο.

ΠΟΥ ΕΙΜΑΣΤΕ ΣΙΓΟΥΡΟΙ ΘΑ ΠΑΤΕ! (αν μάθεις να λύνεις τέτοια παραδείγματα :))

Για παράδειγμα:

Αποφασίστε μόνοι σας:

Ανάλυση λύσεων:

1. Ας ξεκινήσουμε με τον ήδη συνηθισμένο κανόνα για την αύξηση του πτυχίου σε ένα βαθμό:

Δείτε τώρα το σκορ. Σας θυμίζει κάτι; Υπενθυμίζουμε τον τύπο για τον συντομευμένο πολλαπλασιασμό της διαφοράς των τετραγώνων:

Σε αυτήν την περίπτωση,

Τελικά φαίνεται πως:

Απάντηση: .

2. Φέρνουμε κλάσματα σε εκθέτες στην ίδια μορφή: είτε και τα δύο δεκαδικά είτε και τα δύο κοινά. Παίρνουμε, για παράδειγμα:

Απάντηση: 16

3. Τίποτα το ιδιαίτερο, εφαρμόζουμε τις συνήθεις ιδιότητες των πτυχίων:

ΠΡΟΧΩΡΗΜΕΝΟ ΕΠΙΠΕΔΟ

Ορισμός πτυχίου

Ο βαθμός είναι έκφραση της μορφής: , όπου:

— βάση πτυχίου?
- εκθέτης.

Βαθμός με φυσικό εκθέτη (n = 1, 2, 3,...)

Η αύξηση ενός αριθμού στη φυσική ισχύ n σημαίνει πολλαπλασιασμός του αριθμού από τον εαυτό του επί φορές:

Ισχύς με ακέραιο εκθέτη (0, ±1, ±2,...)

Αν ο εκθέτης είναι θετικός ακέραιοςαριθμός:

ανέγερση σε μηδενική ισχύ:

Η έκφραση είναι αόριστη, γιατί, αφενός, σε οποιοδήποτε βαθμό είναι αυτό, και αφετέρου, οποιοσδήποτε αριθμός στον ου βαθμό είναι αυτό.

Αν ο εκθέτης είναι ακέραιος αρνητικόςαριθμός:

(γιατί είναι αδύνατο να διαιρεθεί).

Για άλλη μια φορά για τα μηδενικά: η έκφραση δεν ορίζεται στην περίπτωση. Αν τότε.

Παραδείγματα:

Πτυχίο με ορθολογικό εκθέτη

- φυσικός αριθμός;
είναι ακέραιος αριθμός?

Παραδείγματα:

Ιδιότητες πτυχίου

Για να διευκολύνουμε την επίλυση προβλημάτων, ας προσπαθήσουμε να καταλάβουμε: από πού προήλθαν αυτές οι ιδιότητες; Ας τους αποδείξουμε.

Ας δούμε: τι είναι και;

Εξ ορισμού:

Έτσι, στη δεξιά πλευρά αυτής της έκφρασης, προκύπτει το ακόλουθο προϊόν:

Αλλά εξ ορισμού, αυτή είναι μια δύναμη ενός αριθμού με έναν εκθέτη, δηλαδή:

Q.E.D.

Παράδειγμα : Απλοποιήστε την έκφραση.

Λύση : .

Παράδειγμα : Απλοποιήστε την έκφραση.

Λύση : Είναι σημαντικό να σημειωθεί ότι στον κανόνα μας αναγκαίωςπρέπει να έχουν την ίδια βάση. Επομένως, συνδυάζουμε τις μοίρες με τη βάση, αλλά παραμένουμε ξεχωριστός παράγοντας:

Μια άλλη σημαντική σημείωση: αυτός ο κανόνας - μόνο για προϊόντα δυνάμεων!

Σε καμία περίπτωση δεν πρέπει να το γράψω.

Όπως και με την προηγούμενη ιδιότητα, ας στραφούμε στον ορισμό του πτυχίου:

Ας το αναδιατάξουμε ως εξής:

Αποδεικνύεται ότι η έκφραση πολλαπλασιάζεται από μόνη της μία φορά, δηλαδή, σύμφωνα με τον ορισμό, αυτή είναι η -η δύναμη του αριθμού:

Στην πραγματικότητα, αυτό μπορεί να ονομαστεί "bracketing του δείκτη". Αλλά ποτέ δεν μπορείτε να το κάνετε αυτό συνολικά:!

Ας θυμηθούμε τους τύπους για συντομευμένο πολλαπλασιασμό: πόσες φορές θέλαμε να γράψουμε; Αλλά αυτό δεν είναι αλήθεια, πραγματικά.

Ισχύς με αρνητική βάση.

Μέχρι αυτό το σημείο, έχουμε συζητήσει μόνο τι θα έπρεπε να είναι δείκτηςβαθμός. Ποια πρέπει όμως να είναι η βάση; Σε μοίρες από φυσικός δείκτης η βάση μπορεί να είναι οποιοσδηποτε ΑΡΙΘΜΟΣ .

Πράγματι, μπορούμε να πολλαπλασιάσουμε οποιονδήποτε αριθμό μεταξύ τους, είτε είναι θετικοί, αρνητικοί ή ζυγοί. Ας σκεφτούμε ποια σημάδια (" " ή "") θα έχουν βαθμούς θετικών και αρνητικών αριθμών;

Για παράδειγμα, ο αριθμός θα είναι θετικός ή αρνητικός; ΑΛΛΑ? ?

Με το πρώτο, όλα είναι ξεκάθαρα: ανεξάρτητα από το πόσους θετικούς αριθμούς πολλαπλασιάζουμε μεταξύ τους, το αποτέλεσμα θα είναι θετικό.

Αλλά τα αρνητικά είναι λίγο πιο ενδιαφέροντα. Εξάλλου, θυμόμαστε έναν απλό κανόνα από την 6η δημοτικού: «το μείον επί το μείον δίνει ένα συν». Δηλαδή ή. Αλλά αν πολλαπλασιάσουμε με (), παίρνουμε -.

Και ούτω καθεξής ad infinitum: με κάθε επόμενο πολλαπλασιασμό, το πρόσημο θα αλλάζει. Είναι δυνατό να διατυπωθεί τέτοια απλούς κανόνες:

ακόμη καιβαθμός, - αριθμός θετικός.
Ο αρνητικός αριθμός αυξήθηκε σε Περιττόςβαθμός, - αριθμός αρνητικός.
Ένας θετικός αριθμός σε οποιαδήποτε δύναμη είναι ένας θετικός αριθμός.
Το μηδέν σε οποιαδήποτε ισχύ ισούται με μηδέν.

Προσδιορίστε μόνοι σας τι πρόσημο θα έχουν οι παρακάτω εκφράσεις:

1.	2.	3.
4.	5.	6.

Κατάφερες? Εδώ είναι οι απαντήσεις:

1) ; 2) ; 3) ; 4) ; 5) ; 6) .

Στα πρώτα τέσσερα παραδείγματα, ελπίζω ότι όλα είναι ξεκάθαρα; Απλώς κοιτάμε τη βάση και τον εκθέτη και εφαρμόζουμε τον κατάλληλο κανόνα.

Στο παράδειγμα 5), όλα δεν είναι επίσης τόσο τρομακτικά όσο φαίνονται: δεν έχει σημασία ποια είναι η βάση - ο βαθμός είναι άρτιος, πράγμα που σημαίνει ότι το αποτέλεσμα θα είναι πάντα θετικό. Λοιπόν, εκτός από την περίπτωση που η βάση είναι μηδέν. Η βάση δεν είναι η ίδια, έτσι; Προφανώς όχι, αφού (γιατί).

Το Παράδειγμα 6) δεν είναι πλέον τόσο απλό. Εδώ πρέπει να μάθετε ποιο είναι λιγότερο: ή; Αν το θυμάστε αυτό, γίνεται σαφές ότι, πράγμα που σημαίνει ότι η βάση είναι μικρότερη από το μηδέν. Δηλαδή, εφαρμόζουμε τον κανόνα 2: το αποτέλεσμα θα είναι αρνητικό.

Και πάλι χρησιμοποιούμε τον ορισμό του πτυχίου:

Όλα είναι ως συνήθως - γράφουμε τον ορισμό των βαθμών και τους χωρίζουμε ο ένας στον άλλο, τους χωρίζουμε σε ζεύγη και παίρνουμε:

Πριν αναλύσουμε τον τελευταίο κανόνα, ας λύσουμε μερικά παραδείγματα.

Υπολογίστε τις τιμές των παραστάσεων:

Λύσεις :

Παίρνουμε:

Εξετάζουμε προσεκτικά τον παρονομαστή. Μοιάζει πολύ με έναν από τους αριθμητικούς παράγοντες, αλλά τι φταίει; Λανθασμένη σειρά όρων. Αν αντιστραφούν, θα μπορούσε να εφαρμοστεί ο κανόνας 3. Πώς γίνεται όμως αυτό; Αποδεικνύεται ότι είναι πολύ εύκολο: ο άρτιος βαθμός του παρονομαστή μας βοηθά εδώ.

Αν το πολλαπλασιάσετε επί, δεν αλλάζει τίποτα, σωστά; Τώρα όμως μοιάζει με αυτό:

Οι όροι έχουν αλλάξει τόπους ως δια μαγείας. Αυτό το «φαινόμενο» ισχύει για οποιαδήποτε έκφραση σε άρτιο βαθμό: μπορούμε ελεύθερα να αλλάξουμε τα σημάδια σε αγκύλες. Αλλά είναι σημαντικό να θυμάστε: όλα τα ζώδια αλλάζουν ταυτόχρονα!Δεν μπορεί να αντικατασταθεί αλλάζοντας μόνο ένα απαράδεκτο μείον για εμάς!

Ας επιστρέψουμε στο παράδειγμα:

Και πάλι ο τύπος:

Λοιπόν τώρα ο τελευταίος κανόνας:

Πώς θα το αποδείξουμε; Φυσικά, ως συνήθως: ας επεκτείνουμε την έννοια του πτυχίου και ας απλοποιήσουμε:

Λοιπόν, τώρα ας ανοίξουμε τις αγκύλες. Πόσα γράμματα θα είναι; φορές με πολλαπλασιαστές - πώς μοιάζει; Αυτό δεν είναι παρά ο ορισμός μιας πράξης πολλαπλασιασμός: συνολικά αποδείχθηκαν πολλαπλασιαστές. Δηλαδή, είναι εξ ορισμού δύναμη ενός αριθμού με εκθέτη:

Παράδειγμα:

Πτυχίο με παράλογο εκθέτη

Εκτός από πληροφορίες σχετικά με τους βαθμούς για το μέσο επίπεδο, θα αναλύσουμε το πτυχίο με έναν παράλογο δείκτη. Όλοι οι κανόνες και οι ιδιότητες των βαθμών εδώ είναι ακριβώς οι ίδιοι όπως για έναν βαθμό με λογικό εκθέτη, με εξαίρεση - εξάλλου, εξ ορισμού, οι παράλογοι αριθμοί είναι αριθμοί που δεν μπορούν να αναπαρασταθούν ως κλάσμα, όπου και είναι ακέραιοι (δηλ. , οι παράλογοι αριθμοί είναι όλοι οι πραγματικοί αριθμοί εκτός από τους ορθολογικούς).

Όταν μελετάμε πτυχία με φυσικό, ακέραιο και ορθολογικό δείκτη, κάθε φορά φτιάχναμε μια συγκεκριμένη «εικόνα», «αναλογία» ή περιγραφή με πιο οικείους όρους. Για παράδειγμα, ένας φυσικός εκθέτης είναι ένας αριθμός πολλαπλασιασμένος από τον εαυτό του πολλές φορές. ένας αριθμός στον μηδενικό βαθμό είναι, σαν να λέγαμε, ένας αριθμός πολλαπλασιασμένος από τον εαυτό του μία φορά, δηλαδή, δεν έχει αρχίσει ακόμη να πολλαπλασιάζεται, πράγμα που σημαίνει ότι ο ίδιος ο αριθμός δεν έχει καν εμφανιστεί ακόμα - επομένως, το αποτέλεσμα είναι μόνο ένα ορισμένη «προετοιμασία ενός αριθμού», δηλαδή ένας αριθμός· ένας βαθμός με ακέραιο αρνητικό δείκτη - είναι σαν να έχει συμβεί μια συγκεκριμένη "αντίστροφη διαδικασία", δηλαδή ο αριθμός δεν πολλαπλασιάστηκε από μόνος του, αλλά διαιρέθηκε.

Είναι εξαιρετικά δύσκολο να φανταστεί κανείς έναν βαθμό με έναν παράλογο εκθέτη (όπως είναι δύσκολο να φανταστεί κανείς έναν 4-διάστατο χώρο). Μάλλον, είναι ένα καθαρά μαθηματικό αντικείμενο που δημιούργησαν οι μαθηματικοί για να επεκτείνουν την έννοια του βαθμού σε ολόκληρο τον χώρο των αριθμών.

Παρεμπιπτόντως, η επιστήμη χρησιμοποιεί συχνά έναν βαθμό με σύνθετο εκθέτη, δηλαδή, ένας εκθέτης δεν είναι καν πραγματικός αριθμός. Αλλά στο σχολείο, δεν σκεφτόμαστε τέτοιες δυσκολίες· θα έχετε την ευκαιρία να κατανοήσετε αυτές τις νέες έννοιες στο ινστιτούτο.

Τι κάνουμε λοιπόν αν δούμε έναν παράλογο εκθέτη; Προσπαθούμε να το ξεφορτωθούμε! :)

Για παράδειγμα:

Αποφασίστε μόνοι σας:

Απαντήσεις:

Θυμηθείτε τη διαφορά των τετραγώνων. Απάντηση: .
Φέρνουμε τα κλάσματα στην ίδια μορφή: είτε και τα δύο δεκαδικά είτε και τα δύο συνηθισμένα. Παίρνουμε, για παράδειγμα: .
Τίποτα το ιδιαίτερο, εφαρμόζουμε τις συνήθεις ιδιότητες των πτυχίων:

ΠΕΡΙΛΗΨΗ ΕΝΟΤΗΤΑΣ ΚΑΙ ΒΑΣΙΚΟΣ ΤΥΠΟΣ

Βαθμόςονομάζεται έκφραση της μορφής: , όπου:

Βαθμός με ακέραιο εκθέτη

βαθμός, ο εκθέτης του οποίου είναι ένας φυσικός αριθμός (δηλαδή ακέραιος και θετικός).

Πτυχίο με ορθολογικό εκθέτη

βαθμό, ο δείκτης του οποίου είναι αρνητικοί και κλασματικοί αριθμοί.

Πτυχίο με παράλογο εκθέτη

εκθέτης του οποίου ο εκθέτης είναι ένα άπειρο δεκαδικό κλάσμα ή ρίζα.

Ιδιότητες πτυχίου

Χαρακτηριστικά πτυχίων.

Ο αρνητικός αριθμός αυξήθηκε σε ακόμη καιβαθμός, - αριθμός θετικός.
Ο αρνητικός αριθμός αυξήθηκε σε Περιττόςβαθμός, - αριθμός αρνητικός.
Ένας θετικός αριθμός σε οποιαδήποτε δύναμη είναι ένας θετικός αριθμός.
Το μηδέν ισούται με οποιαδήποτε δύναμη.
Οποιοσδήποτε αριθμός στη μηδενική ισχύ είναι ίσος.

ΤΩΡΑ ΕΧΕΙΣ ΛΟΓΙΑ...

Πώς σας φαίνεται το άρθρο; Ενημερώστε με στα σχόλια παρακάτω αν σας άρεσε ή όχι.

Πείτε μας για την εμπειρία σας με τις ιδιότητες ισχύος.

Ίσως έχετε ερωτήσεις. Ή προτάσεις.

Γράψτε στα σχόλια.

Και καλή επιτυχία στις εξετάσεις σας!

Σημειώστε ότι αυτή η ενότητα ασχολείται με την έννοια μοίρες μόνο με φυσικό δείκτηκαι μηδέν.

Η έννοια και οι ιδιότητες των βαθμών με ορθολογικούς εκθέτες (με αρνητικούς και κλασματικούς) θα συζητηθούν στα μαθήματα για την 8η τάξη.

Λοιπόν, ας καταλάβουμε ποιος είναι ο βαθμός ενός αριθμού.Για να γράψετε το γινόμενο ενός αριθμού από μόνο του, η συντομευμένη σημείωση χρησιμοποιείται πολλές φορές.

Αντί να πολλαπλασιάσουν έξι πανομοιότυπους παράγοντες 4 4 4 4 4 4 γράφουν 4 6 και λένε "τέσσερα στην έκτη δύναμη".

4 4 4 4 4 4 = 4 6

Η έκφραση 4 6 ονομάζεται δύναμη ενός αριθμού, όπου:

4 — βάση πτυχίου;
6 — εκθέτης.

Γενικά, ο βαθμός με τη βάση "a" και τον εκθέτη "n" γράφεται χρησιμοποιώντας την έκφραση:

Θυμάμαι!

Ο βαθμός του αριθμού "a" με φυσικό εκθέτη "n", μεγαλύτερο από 1, είναι το γινόμενο "n" πανομοιότυποι παράγοντες, καθένας από τους οποίους είναι ίσος με τον αριθμό "a".

Η εγγραφή " a n"Διαβάζεται ως εξής:" και στην ισχύ n "ή" n-η δύναμη του αριθμού a".

Οι εξαιρέσεις είναι οι εγγραφές:

a 2 - μπορεί να προφερθεί ως "a τετράγωνο".
a 3 - μπορεί να προφερθεί ως "a σε έναν κύβο".

α 2 - "και στον δεύτερο βαθμό"?
α 3 - "α στον τρίτο βαθμό."

Ειδικές περιπτώσεις προκύπτουν εάν ο εκθέτης είναι ίσος με ένα ή μηδέν (n = 1, n = 0).

Θυμάμαι!

Ο βαθμός του αριθμού "a" με τον εκθέτη n \u003d 1 είναι αυτός ο ίδιος ο αριθμός:
α 1 = α

Οποιοσδήποτε αριθμός στη μηδενική ισχύ είναι ίσος με ένα.
a 0 = 1

Το μηδέν σε οποιαδήποτε φυσική ισχύ ισούται με μηδέν.
0 n = 0

Ένα προς οποιαδήποτε δύναμη ισούται με 1.
1n=1

Έκφραση 0 0 ( μηδενική έως μηδενική ισχύς) θεωρείται ανούσιο.

(−32) 0 = 1
0 253 = 0
1 4 = 1

Όταν λύνετε παραδείγματα, πρέπει να θυμάστε ότι η αύξηση σε μια ισχύ ονομάζεται εύρεση μιας αριθμητικής ή κυριολεκτικής τιμής μετά την αύξηση της σε μια ισχύ.

Παράδειγμα. Ανέβασε σε δύναμη.

5 3 = 5 5 5 = 125
2,5 2 = 2,5 2,5 = 6,25
( · = = 81
256

Εκτίμηση αρνητικού αριθμού

Η βάση της ισχύος (ο αριθμός που αυξάνεται σε δύναμη) μπορεί να είναι οποιοσδήποτε αριθμός — θετικός, αρνητικός ή μηδέν.

Θυμάμαι!

Η αύξηση ενός θετικού αριθμού σε μια ισχύ οδηγεί σε έναν θετικό αριθμό.

Η αύξηση του μηδέν σε μια φυσική ισχύ οδηγεί σε μηδέν.

Όταν αυξάνεται ένας αρνητικός αριθμός σε δύναμη, το αποτέλεσμα μπορεί να είναι είτε θετικός είτε αρνητικός αριθμός. Εξαρτάται από το αν ο εκθέτης ήταν άρτιος ή περιττός αριθμός.

Εξετάστε παραδείγματα αύξησης αρνητικών αριθμών σε δύναμη.

Μπορεί να φανεί από τα παραδείγματα που εξετάστηκαν ότι εάν ένας αρνητικός αριθμός αυξηθεί σε περιττή ισχύ, τότε προκύπτει ένας αρνητικός αριθμός. Αφού το γινόμενο ενός περιττού αριθμού αρνητικών παραγόντων είναι αρνητικό.

Εάν ένας αρνητικός αριθμός αυξηθεί σε άρτια ισχύ, τότε προκύπτει ένας θετικός αριθμός. Αφού το γινόμενο ενός ζυγού αριθμού αρνητικών παραγόντων είναι θετικό.

Θυμάμαι!

Ένας αρνητικός αριθμός που αυξάνεται σε άρτια ισχύ είναι θετικός αριθμός.

Ένας αρνητικός αριθμός που αυξάνεται σε περιττή ισχύ είναι αρνητικός αριθμός.

Το τετράγωνο οποιουδήποτε αριθμού είναι θετικός αριθμός ή μηδέν, δηλαδή:

a 2 ≥ 0 για οποιοδήποτε a .

2 (−3) 2 = 2 (−3) (−3) = 2 9 = 18
−5 (−2) 3 = −5 (−8) = 40

Σημείωση!

Κατά την επίλυση παραδειγμάτων εκθέσεως, γίνονται συχνά λάθη, ξεχνώντας ότι οι εγγραφές (−5) 4 και −5 4 είναι διαφορετικές εκφράσεις. Τα αποτελέσματα της αύξησης σε μια δύναμη αυτών των εκφράσεων θα είναι διαφορετικά.

Υπολογίστε (−5) 4 σημαίνει να βρείτε την τιμή της τέταρτης δύναμης ενός αρνητικού αριθμού.

(−5) 4 = (−5) (−5) (−5) (−5) = 625

Ενώ η εύρεση του "-5 4" σημαίνει ότι το παράδειγμα πρέπει να λυθεί σε 2 βήματα:

Ανεβάστε τον θετικό αριθμό 5 στην τέταρτη δύναμη.
5 4 = 5 5 5 5 = 625
Βάλτε ένα σύμβολο μείον μπροστά από το αποτέλεσμα που προκύπτει (δηλαδή εκτελέστε μια ενέργεια αφαίρεσης).
−5 4 = −625

Παράδειγμα. Υπολογίστε: −6 2 − (−1) 4

−6 2 − (−1) 4 = −37

6 2 = 6 6 = 36
−6 2 = −36
(−1) 4 = (−1) (−1) (−1) (−1) = 1
−(−1) 4 = −1
−36 − 1 = −37

Διαδικασία για παραδείγματα με πτυχία

Ο υπολογισμός μιας τιμής ονομάζεται ενέργεια της εκθεσιμότητας. Αυτή είναι η δράση του τρίτου σταδίου.

Θυμάμαι!

Σε εκφράσεις με μοίρες που δεν περιέχουν αγκύλες, εκτελέστε πρώτα εκθέσεως, έπειτα πολλαπλασιασμός και διαίρεση, και στο τέλος πρόσθεση και αφαίρεση.

Εάν υπάρχουν αγκύλες στην έκφραση, τότε πρώτα, με τη σειρά που υποδεικνύεται παραπάνω, εκτελούνται οι ενέργειες στις αγκύλες και, στη συνέχεια, οι υπόλοιπες ενέργειες με την ίδια σειρά από αριστερά προς τα δεξιά.

Παράδειγμα. Υπολογίζω:

Για τη διευκόλυνση της επίλυσης παραδειγμάτων, είναι χρήσιμο να γνωρίζετε και να χρησιμοποιείτε τον πίνακα πτυχίων, τον οποίο μπορείτε να κατεβάσετε δωρεάν στην ιστοσελίδα μας.

Για να ελέγξετε τα αποτελέσματά σας, μπορείτε να χρησιμοποιήσετε την αριθμομηχανή στον ιστότοπό μας "

Καταλάβαμε γενικά ποιος είναι ο βαθμός ενός αριθμού. Τώρα πρέπει να καταλάβουμε πώς να το υπολογίσουμε σωστά, δηλ. ανεβάσουν τους αριθμούς σε δυνάμεις. Σε αυτό το υλικό, θα αναλύσουμε τους βασικούς κανόνες για τον υπολογισμό του βαθμού στην περίπτωση ενός ακέραιου, φυσικού, κλασματικού, ορθολογικού και παράλογου εκθέτη. Όλοι οι ορισμοί θα επεξηγηθούν με παραδείγματα.

Η έννοια της εκθέσεως

Ας ξεκινήσουμε με τη διατύπωση βασικών ορισμών.

Ορισμός 1

Εκθεσιμότηταείναι ο υπολογισμός της τιμής της ισχύος κάποιου αριθμού.

Δηλαδή, οι λέξεις «υπολογισμός της αξίας του βαθμού» και «εκθετική» σημαίνουν το ίδιο πράγμα. Έτσι, εάν η εργασία είναι "Αύξηση του αριθμού 0 , 5 στην πέμπτη δύναμη", αυτό θα πρέπει να γίνει κατανοητό ως "υπολογίστε την τιμή της ισχύος (0 , 5) 5 .

Τώρα δίνουμε τους βασικούς κανόνες που πρέπει να ακολουθούνται σε τέτοιους υπολογισμούς.

Θυμηθείτε τι είναι η δύναμη ενός αριθμού με φυσικό εκθέτη. Για μια ισχύ με βάση a και εκθέτη n, αυτό θα είναι το γινόμενο του nου αριθμού παραγόντων, καθένας από τους οποίους είναι ίσος με a. Αυτό μπορεί να γραφτεί ως εξής:

Για να υπολογίσετε την τιμή του βαθμού, πρέπει να εκτελέσετε τη λειτουργία του πολλαπλασιασμού, δηλαδή να πολλαπλασιάσετε τις βάσεις του βαθμού τον καθορισμένο αριθμό φορών. Η ίδια η έννοια ενός πτυχίου με φυσικό δείκτη βασίζεται στην ικανότητα γρήγορου πολλαπλασιασμού. Ας δώσουμε παραδείγματα.

Παράδειγμα 1

Κατάσταση: Ανύψωση - 2 στην ισχύ του 4 .

Λύση

Χρησιμοποιώντας τον παραπάνω ορισμό, γράφουμε: (− 2) 4 = (− 2) (− 2) (− 2) (− 2) . Στη συνέχεια, πρέπει απλώς να ακολουθήσουμε αυτά τα βήματα και να πάρουμε 16 .

Ας πάρουμε ένα πιο περίπλοκο παράδειγμα.

Παράδειγμα 2

Υπολογίστε την τιμή 3 2 7 2

Λύση

Αυτή η καταχώρηση μπορεί να ξαναγραφτεί ως 3 2 7 · 3 2 7 . Νωρίτερα εξετάσαμε πώς να πολλαπλασιάσουμε σωστά τους μικτούς αριθμούς που αναφέρονται στη συνθήκη.

Εκτελέστε αυτά τα βήματα και λάβετε την απάντηση: 3 2 7 3 2 7 = 23 7 23 7 = 529 49 = 10 39 49

Εάν η εργασία υποδεικνύει την ανάγκη αύξησης των παράλογων αριθμών σε μια φυσική ισχύ, θα πρέπει πρώτα να στρογγυλοποιήσουμε τις βάσεις τους σε ένα ψηφίο που θα μας επιτρέψει να λάβουμε μια απάντηση της επιθυμητής ακρίβειας. Ας πάρουμε ένα παράδειγμα.

Παράδειγμα 3

Εκτελέστε τον τετραγωνισμό του αριθμού π .

Λύση

Ας το στρογγυλοποιήσουμε πρώτα στα εκατοστά. Τότε π 2 ≈ (3, 14) 2 = 9, 8596. Αν π ≈ 3 . 14159, τότε θα έχουμε ένα πιο ακριβές αποτέλεσμα: π 2 ≈ (3, 14159) 2 = 9, 8695877281.

Σημειώστε ότι η ανάγκη υπολογισμού των δυνάμεων των παράλογων αριθμών στην πράξη προκύπτει σχετικά σπάνια. Μπορούμε στη συνέχεια να γράψουμε την απάντηση ως την ίδια την ισχύ (ln 6) 3 ή να μετατρέψουμε αν είναι δυνατόν: 5 7 = 125 5 .

Ξεχωριστά, θα πρέπει να αναφέρεται ποια είναι η πρώτη δύναμη ενός αριθμού. Εδώ μπορείτε απλώς να θυμάστε ότι οποιοσδήποτε αριθμός αυξηθεί στην πρώτη δύναμη θα παραμείνει ο ίδιος:

Αυτό είναι ξεκάθαρο από το αρχείο. .

Δεν εξαρτάται από τη βάση του πτυχίου.

Παράδειγμα 4

Άρα, (− 9) 1 = − 9 , και το 7 3 ανυψωμένο στην πρώτη δύναμη παραμένει ίσο με 7 3 .

Για ευκολία, θα αναλύσουμε τρεις περιπτώσεις χωριστά: αν ο εκθέτης είναι θετικός ακέραιος, αν είναι μηδέν και αν είναι αρνητικός ακέραιος.

Στην πρώτη περίπτωση, αυτό είναι το ίδιο με την αύξηση σε μια φυσική δύναμη: τελικά, οι θετικοί ακέραιοι ανήκουν στο σύνολο των φυσικών αριθμών. Έχουμε ήδη περιγράψει τον τρόπο εργασίας με τέτοιους τίτλους σπουδών παραπάνω.

Τώρα ας δούμε πώς να αυξήσετε σωστά τη μηδενική ισχύ. Με μια βάση που δεν είναι μηδενική, αυτός ο υπολογισμός παράγει πάντα μια έξοδο 1 . Έχουμε εξηγήσει προηγουμένως ότι η 0η δύναμη του a μπορεί να οριστεί για οποιονδήποτε πραγματικό αριθμό που δεν ισούται με 0, και a 0 = 1.

Παράδειγμα 5

5 0 = 1 , (- 2 , 56) 0 = 1 2 3 0 = 1

0 0 - δεν ορίζεται.

Μας μένει μόνο η περίπτωση ενός βαθμού με αρνητικό ακέραιο εκθέτη. Έχουμε ήδη συζητήσει ότι τέτοιοι βαθμοί μπορούν να γραφτούν ως κλάσμα 1 a z, όπου a είναι οποιοσδήποτε αριθμός και z είναι αρνητικός ακέραιος. Βλέπουμε ότι ο παρονομαστής αυτού του κλάσματος δεν είναι παρά ένας συνηθισμένος βαθμός με θετικό ακέραιο και έχουμε ήδη μάθει πώς να τον υπολογίζουμε. Ας δώσουμε παραδείγματα εργασιών.

Παράδειγμα 6

Ανεβάστε το 2 στην ισχύ -3.

Λύση

Χρησιμοποιώντας τον παραπάνω ορισμό, γράφουμε: 2 - 3 = 1 2 3

Υπολογίζουμε τον παρονομαστή αυτού του κλάσματος και παίρνουμε 8: 2 3 \u003d 2 2 2 \u003d 8.

Τότε η απάντηση είναι: 2 - 3 = 1 2 3 = 1 8

Παράδειγμα 7

Ανεβάστε το 1, 43 στην ισχύ -2.

Λύση

Αναδιατύπωση: 1 , 43 - 2 = 1 (1 , 43) 2

Υπολογίζουμε το τετράγωνο στον παρονομαστή: 1,43 1,43. Οι δεκαδικοί μπορούν να πολλαπλασιαστούν με αυτόν τον τρόπο: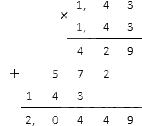

Ως αποτέλεσμα, πήραμε (1, 43) - 2 = 1 (1, 43) 2 = 1 2 , 0449 . Απομένει να γράψουμε αυτό το αποτέλεσμα με τη μορφή ενός συνηθισμένου κλάσματος, για το οποίο είναι απαραίτητο να το πολλαπλασιάσουμε με 10 χιλιάδες (δείτε το υλικό για τη μετατροπή των κλασμάτων).

Απάντηση: (1, 43) - 2 = 10000 20449

Μια ξεχωριστή περίπτωση είναι η αύξηση ενός αριθμού στην μείον πρώτη δύναμη. Η τιμή ενός τέτοιου βαθμού είναι ίση με τον αριθμό αντίθετο από την αρχική τιμή της βάσης: a - 1 \u003d 1 a 1 \u003d 1 a.

Παράδειγμα 8

Παράδειγμα: 3 − 1 = 1 / 3

9 13 - 1 = 13 9 6 4 - 1 = 1 6 4 .

Πώς να αυξήσετε έναν αριθμό σε κλασματική δύναμη

Για να εκτελέσουμε μια τέτοια πράξη, πρέπει να θυμηθούμε τον βασικό ορισμό ενός βαθμού με κλασματικό εκθέτη: a m n \u003d a m n για κάθε θετικό a, ακέραιο m και φυσικό n.

Ορισμός 2

Έτσι, ο υπολογισμός ενός κλασματικού βαθμού πρέπει να εκτελεστεί σε δύο βήματα: αύξηση σε ακέραιο αριθμό και εύρεση της ρίζας του nου βαθμού.

Έχουμε την ισότητα a m n = a m n , η οποία, δεδομένων των ιδιοτήτων των ριζών, χρησιμοποιείται συνήθως για την επίλυση προβλημάτων με τη μορφή a m n = a n m . Αυτό σημαίνει ότι αν αυξήσουμε τον αριθμό a σε μια κλασματική ισχύ m / n, τότε πρώτα εξάγουμε τη ρίζα του nου βαθμού από το a, μετά ανεβάζουμε το αποτέλεσμα σε δύναμη με ακέραιο εκθέτη m.

Ας το διευκρινίσουμε με ένα παράδειγμα.

Παράδειγμα 9

Υπολογίστε 8 - 2 3 .

Λύση

Μέθοδος 1. Σύμφωνα με τον βασικό ορισμό, μπορούμε να το αναπαραστήσουμε ως: 8 - 2 3 \u003d 8 - 2 3

Τώρα ας υπολογίσουμε τον βαθμό κάτω από τη ρίζα και ας εξαγάγουμε την τρίτη ρίζα από το αποτέλεσμα: 8 - 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4

Μέθοδος 2. Ας μετατρέψουμε τη βασική ισότητα: 8 - 2 3 \u003d 8 - 2 3 \u003d 8 3 - 2

Μετά από αυτό, εξάγουμε τη ρίζα 8 3 - 2 = 2 3 3 - 2 = 2 - 2 και τετραγωνίζουμε το αποτέλεσμα: 2 - 2 = 1 2 2 = 1 4

Βλέπουμε ότι οι λύσεις είναι πανομοιότυπες. Μπορείτε να χρησιμοποιήσετε όποιον τρόπο θέλετε.

Υπάρχουν περιπτώσεις που ο βαθμός έχει δείκτη που εκφράζεται ως μικτός αριθμός ή δεκαδικό κλάσμα. Για ευκολία υπολογισμού, είναι καλύτερο να το αντικαταστήσετε με ένα συνηθισμένο κλάσμα και να μετρήσετε όπως υποδεικνύεται παραπάνω.

Παράδειγμα 10

Ανεβάστε το 44,89 στη δύναμη του 2,5.

Λύση

Ας μετατρέψουμε την τιμή του δείκτη σε ένα συνηθισμένο κλάσμα: 44 , 89 2 , 5 = 44 , 89 5 2 .

Και τώρα εκτελούμε όλες τις ενέργειες που υποδεικνύονται παραπάνω με τη σειρά: 44 , 89 5 2 = 44 , 89 5 = 44 , 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 501 = 67 10 501 = 20 13 501, 25107

Απάντηση: 13501, 25107.

Εάν υπάρχουν μεγάλοι αριθμοί στον αριθμητή και στον παρονομαστή ενός κλασματικού εκθέτη, τότε ο υπολογισμός τέτοιων εκθετών με ορθολογικούς εκθέτες είναι μια αρκετά δύσκολη δουλειά. Συνήθως απαιτεί τεχνολογία υπολογιστών.

Ξεχωριστά, μένουμε στον βαθμό με μηδενική βάση και κλασματικό εκθέτη. Σε μια έκφραση της μορφής 0 m n μπορεί να δοθεί η ακόλουθη έννοια: εάν m n > 0, τότε 0 m n = 0 m n = 0 ; αν m n< 0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0 7 12 = 0 , 0 3 2 5 = 0 , 0 0 , 024 = 0 , а в целую отрицательную - значения не имеет: 0 - 4 3 .

Πώς να αυξήσετε έναν αριθμό σε μια παράλογη δύναμη

Η ανάγκη υπολογισμού της τιμής του βαθμού, στον δείκτη του οποίου υπάρχει ένας παράλογος αριθμός, δεν προκύπτει τόσο συχνά. Στην πράξη, η εργασία συνήθως περιορίζεται στον υπολογισμό μιας κατά προσέγγιση τιμής (μέχρι ένα ορισμένο αριθμό δεκαδικών ψηφίων). Αυτό συνήθως υπολογίζεται σε υπολογιστή λόγω της πολυπλοκότητας τέτοιων υπολογισμών, επομένως δεν θα σταθούμε λεπτομερώς σε αυτό, θα αναφέρουμε μόνο τις κύριες διατάξεις.

Εάν πρέπει να υπολογίσουμε την τιμή του βαθμού a με έναν παράλογο εκθέτη a , τότε παίρνουμε τη δεκαδική προσέγγιση του εκθέτη και μετράμε από αυτήν. Το αποτέλεσμα θα είναι μια κατά προσέγγιση απάντηση. Όσο πιο ακριβής είναι η δεκαδική προσέγγιση, τόσο πιο ακριβής είναι η απάντηση. Ας δείξουμε με ένα παράδειγμα:

Παράδειγμα 11

Υπολογίστε την κατά προσέγγιση τιμή του 2 στην ισχύ του 1,174367....

Λύση

Περιοριζόμαστε στη δεκαδική προσέγγιση a n = 1 , 17 . Ας κάνουμε τους υπολογισμούς χρησιμοποιώντας αυτόν τον αριθμό: 2 1 , 17 ≈ 2 , 250116 . Αν πάρουμε, για παράδειγμα, την προσέγγιση a n = 1 , 1743 , τότε η απάντηση θα είναι λίγο πιο ακριβής: 2 1 , 174367 . . . ≈ 2 1. 1743 ≈ 2. 256833.

Εάν παρατηρήσετε κάποιο λάθος στο κείμενο, επισημάνετε το και πατήστε Ctrl+Enter

Σας υπενθυμίζουμε ότι σε αυτό το μάθημα καταλαβαίνουμε ιδιότητες βαθμούμε φυσικούς δείκτες και μηδέν. Τα πτυχία με ορθολογικούς δείκτες και οι ιδιότητές τους θα συζητηθούν στα μαθήματα για την 8η τάξη.

Ένας εκθέτης με φυσικό εκθέτη έχει πολλές σημαντικές ιδιότητες που σας επιτρέπουν να απλοποιήσετε τους υπολογισμούς σε παραδείγματα εκθέτη.

Ακίνητο #1
Προϊόν των δυνάμεων

Θυμάμαι!

Όταν πολλαπλασιάζονται οι δυνάμεις με την ίδια βάση, η βάση παραμένει αμετάβλητη και οι εκθέτες προστίθενται.

a m a n \u003d a m + n, όπου "a"- οποιοσδήποτε αριθμός και" m", "n" - οποιοιδήποτε φυσικοί αριθμοί.

Αυτή η ιδιότητα των δυνάμεων επηρεάζει επίσης το γινόμενο τριών ή περισσότερων δυνάμεων.

Απλοποιήστε την έκφραση.
b b 2 b 3 b 4 b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
Παρουσιάστε ως πτυχίο.
6 15 36 = 6 15 6 2 = 6 15 6 2 = 6 17
Παρουσιάστε ως πτυχίο.
(0,8) 3 (0,8) 12 = (0,8) 3 + 12 = (0,8) 15

Σπουδαίος!

Λάβετε υπόψη ότι στην υποδεικνυόμενη ιδιότητα αφορούσε μόνο τον πολλαπλασιασμό των δυνάμεων με τους ίδιους λόγους . Δεν ισχύει για την προσθήκη τους.

Δεν μπορείτε να αντικαταστήσετε το άθροισμα (3 3 + 3 2) με 3 5 . Αυτό είναι κατανοητό αν
υπολογίστε (3 3 + 3 2) = (27 + 9) = 36 και 3 5 = 243

Ακίνητο #2
Ιδιωτικά πτυχία

Θυμάμαι!

Κατά τη διαίρεση των δυνάμεων με την ίδια βάση, η βάση παραμένει αμετάβλητη και ο εκθέτης του διαιρέτη αφαιρείται από τον εκθέτη του μερίσματος.

= 11 3 − 2 4 2 − 1 = 11 4 = 44

Παράδειγμα. Λύστε την εξίσωση. Χρησιμοποιούμε την ιδιότητα των μερικών μοιρών.
3 8: t = 3 4

T = 3 8 − 4

Απάντηση: t = 3 4 = 81

Χρησιμοποιώντας τις ιδιότητες Νο. 1 και Νο. 2, μπορείτε εύκολα να απλοποιήσετε εκφράσεις και να εκτελέσετε υπολογισμούς.

Παράδειγμα. Απλοποιήστε την έκφραση.
4 5m + 6 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
Παράδειγμα. Βρείτε την τιμή μιας παράστασης χρησιμοποιώντας ιδιότητες βαθμού.
= = = 2 9 + 2
2 5
= 2 11
2 5
= 2 11 − 5 = 2 6 = 64
Σπουδαίος!
Λάβετε υπόψη ότι η ιδιοκτησία 2 αφορούσε μόνο την κατανομή εξουσιών με τις ίδιες βάσεις.

Δεν μπορείτε να αντικαταστήσετε τη διαφορά (4 3 −4 2) με 4 1 . Αυτό είναι κατανοητό αν αναλογιστούμε (4 3 −4 2) = (64 − 16) = 48 και 4 1 = 4

Πρόσεχε!

Ακίνητο #3
Εκθεσιμότητα

Θυμάμαι!
Κατά την αύξηση της ισχύος σε μια ισχύ, η βάση της ισχύος παραμένει αμετάβλητη και οι εκθέτες πολλαπλασιάζονται.
(a n) m \u003d a n m, όπου "a" είναι οποιοσδήποτε αριθμός και "m", "n" είναι οποιοιδήποτε φυσικοί αριθμοί.

Ιδιότητες 4
Πτυχίο προϊόντος

Θυμάμαι!
Όταν ανεβάζετε ένα προϊόν σε μια ισχύ, κάθε ένας από τους παράγοντες αυξάνεται σε μια ισχύ. Τα αποτελέσματα στη συνέχεια πολλαπλασιάζονται.
(α β) n \u003d a n b n, όπου "a", "b" είναι οποιοιδήποτε ρητικοί αριθμοί. "n" - οποιοσδήποτε φυσικός αριθμός.
- Παράδειγμα 1
  (6 a 2 b 3 c) 2 = 6 2 a 2 2 b 3 2 s 1 2 = 36 a 4 b 6 s 2
- Παράδειγμα 2
  (−x 2 y) 6 = ((−1) 6 x 2 6 y 1 6) = x 12 y 6
Σπουδαίος!
Σημειώστε ότι η ιδιότητα Νο. 4, όπως και άλλες ιδιότητες πτυχίων, εφαρμόζεται επίσης με αντίστροφη σειρά.
(a n b n)= (a b) n
Δηλαδή, για να πολλαπλασιάσετε δυνάμεις με τους ίδιους εκθέτες, μπορείτε να πολλαπλασιάσετε τις βάσεις και να αφήσετε τον εκθέτη αμετάβλητο.
- Παράδειγμα. Υπολογίζω.
  2 4 5 4 = (2 5) 4 = 10 4 = 10.000
- Παράδειγμα. Υπολογίζω.
  0,5 16 2 16 = (0,5 2) 16 = 1
Σε πιο σύνθετα παραδείγματα, μπορεί να υπάρχουν περιπτώσεις όπου ο πολλαπλασιασμός και η διαίρεση πρέπει να εκτελεστούν σε δυνάμεις με διαφορετικές βάσεις και διαφορετικούς εκθέτες. Σε αυτή την περίπτωση, σας συμβουλεύουμε να κάνετε τα εξής.

Για παράδειγμα, 4 5 3 2 = 4 3 4 2 3 2 = 4 3 (4 3) 2 = 64 12 2 = 64 144 = 9216

Παράδειγμα εκθέσεως δεκαδικού κλάσματος.
4 21 (−0,25) 20 = 4 4 20 (−0,25) 20 = 4 (4 (−0,25)) 20 = 4 (−1) 20 = 4 1 = τέσσερα
Ιδιότητες 5
Δύναμη του πηλίκου (κλάσματα)

Θυμάμαι!
Για να αυξήσετε ένα πηλίκο σε μια δύναμη, μπορείτε να αυξήσετε το μέρισμα και τον διαιρέτη ξεχωριστά σε αυτή τη δύναμη και να διαιρέσετε το πρώτο αποτέλεσμα με το δεύτερο.
(α: β) n \u003d a n: b n, όπου "a", "b" είναι οποιοιδήποτε ρητός αριθμός, b ≠ 0, n είναι οποιοσδήποτε φυσικός αριθμός.
- Παράδειγμα. Εκφράστε την έκφραση ως μερικές δυνάμεις.
  (5: 3) 12 = 5 12: 3 12
Υπενθυμίζουμε ότι ένα πηλίκο μπορεί να αναπαρασταθεί ως κλάσμα. Ως εκ τούτου, θα σταθούμε στο θέμα της αύξησης ενός κλάσματος σε μια ισχύ με περισσότερες λεπτομέρειες στην επόμενη σελίδα.

Πρωταρχικός στόχος

Να εξοικειώσει τους μαθητές με τις ιδιότητες των βαθμών με φυσικούς δείκτες και να τους διδάξει να εκτελούν ενέργειες με βαθμούς.

Θέμα «Το πτυχίο και οι ιδιότητές του»περιλαμβάνει τρεις ερωτήσεις:

Προσδιορισμός του πτυχίου με φυσικό δείκτη.
Πολλαπλασιασμός και διαίρεση δυνάμεων.
Εκτίμηση προϊόντος και βαθμού.

ερωτήσεις δοκιμής

Να διατυπώσετε τον ορισμό ενός βαθμού με φυσικό εκθέτη μεγαλύτερο από 1. Δώστε ένα παράδειγμα.
Διατυπώστε έναν ορισμό του βαθμού με δείκτη 1. Δώστε ένα παράδειγμα.
Ποια είναι η σειρά των πράξεων κατά την αξιολόγηση της τιμής μιας έκφρασης που περιέχει δυνάμεις;
Να διατυπώσετε την κύρια ιδιότητα του πτυχίου. Δώσε ένα παράδειγμα.
Διατυπώστε έναν κανόνα για τον πολλαπλασιασμό των δυνάμεων με την ίδια βάση. Δώσε ένα παράδειγμα.
Διατυπώστε έναν κανόνα για τη διαίρεση των δυνάμεων με τις ίδιες βάσεις. Δώσε ένα παράδειγμα.
Να διατυπώσετε τον κανόνα για την εκτίμηση ενός προϊόντος. Δώσε ένα παράδειγμα. Να αποδείξετε την ταυτότητα (ab) n = a n b n .
Διατυπώστε έναν κανόνα για την αύξηση του βαθμού σε μια δύναμη. Δώσε ένα παράδειγμα. Να αποδείξετε την ταυτότητα (a m) n = a m n .

Ορισμός πτυχίου.

βαθμός του αριθμού έναμε φυσικό δείκτη n, μεγαλύτερο από 1, ονομάζεται γινόμενο n παραγόντων, καθένας από τους οποίους είναι ίσος με ένα. βαθμός του αριθμού έναμε εκθέτη 1 καλείται ο ίδιος ο αριθμός ένα.

Πτυχίο με βάση ένακαι δείκτης nγράφεται ως εξής: a n. Διαβάζει " έναστο βαθμό n”? « ν-η δύναμη ενός αριθμού ένα ”.

Εξ ορισμού πτυχίου:

α 4 = α α α α

. . . . . . . . . . . .

Η εύρεση της τιμής του βαθμού ονομάζεται εκθέσεως .

1. Παραδείγματα εκθέσεως:

3 3 = 3 3 3 = 27

0 4 = 0 0 0 0 = 0

(-5) 3 = (-5) (-5) (-5) = -125

25 ; 0,09 ;

25 = 5 2 ; 0,09 = (0,3) 2 ; .

27 ; 0,001 ; 8 .

27 = 3 3 ; 0,001 = (0,1) 3 ; 8 = 2 3 .

4. Βρείτε τιμές παραστάσεων:

α) 3 10 3 = 3 10 10 10 = 3 1000 = 3000

β) -2 4 + (-3) 2 = 7
2 4 = 16
(-3) 2 = 9
-16 + 9 = 7

Επιλογή 1

α) 0,3 0,3 0,3

γ) β β β β β β β

δ) (-x) (-x) (-x) (-x)

ε) (αβ) (αβ) (αβ)

2. Τετράγωνο των αριθμών:

3. Κύβω τους αριθμούς:

4. Βρείτε τιμές παραστάσεων:

γ) -1 4 + (-2) 3

δ) -4 3 + (-3) 2

ε) 100 - 5 2 4

Πολλαπλασιασμός δυνάμεων.

Για οποιονδήποτε αριθμό a και αυθαίρετους αριθμούς m και n, ισχύει το εξής:

a m a n = a m + n .

Απόδειξη:

κανόνας : Όταν πολλαπλασιάζονται οι δυνάμεις με την ίδια βάση, οι βάσεις παραμένουν ίδιες και προστίθενται οι εκθέτες.

a m a n a k = a m + n a k = a (m + n) + k = a m + n + k

α) x 5 x 4 = x 5 + 4 = x 9

β) y y 6 = y 1 y 6 = y 1 + 6 = y 7

γ) b 2 b 5 b 4 \u003d b 2 + 5 + 4 \u003d b 11

δ) 3 4 9 = 3 4 3 2 = 3 6

ε) 0,01 0,1 3 = 0,1 2 0,1 3 = 0,1 5

α) 2 3 2 = 2 4 = 16

β) 3 2 3 5 = 3 7 = 2187

Επιλογή 1

1. Παρουσιάστε ως πτυχίο:

α) x 3 x 4 ε) x 2 x 3 x 4

β) a 6 a 2 g) 3 3 9

γ) y 4 y η) 7 4 49

δ) a a 8 i) 16 2 7

ε) 2 3 2 4 ι) 0,3 3 0,09

2. Παρουσιάστε ως βαθμό και βρείτε την τιμή στον πίνακα:

α) 2 2 2 3 γ) 8 2 5

β) 3 4 3 2 δ) 27 243

Διαίρεση πτυχίων.

Για οποιονδήποτε αριθμό a0 και αυθαίρετους φυσικούς αριθμούς m και n έτσι ώστε m>n, ισχύει το εξής:

a m: a n = a m - n

Απόδειξη:

a m - n a n = a (m - n) + n = a m - n + n = a m

εξ ορισμού του ιδιωτικού:

a m: a n \u003d a m - n.

κανόνας: Κατά τη διαίρεση των δυνάμεων με την ίδια βάση, η βάση μένει ίδια και ο εκθέτης του διαιρέτη αφαιρείται από τον εκθέτη του μερίσματος.

Ορισμός: Ο βαθμός ενός μη μηδενικού αριθμού με μηδενικό εκθέτη είναι ίσος με ένα:

επειδή a n: a n = 1 για a0 .

α) x 4: x 2 \u003d x 4 - 2 \u003d x 2

β) y 8: y 3 = y 8 - 3 = y 5

γ) a 7: a \u003d a 7: a 1 \u003d a 7 - 1 \u003d a 6

δ) s 5:s 0 = s 5:1 = s 5

α) 5 7:5 5 = 5 2 = 25

β) 10 20:10 17 = 10 3 = 1000

σε)

ΣΟΛ)

μι)

Επιλογή 1

1. Εκφράστε το πηλίκο ως δύναμη:

2. Βρείτε τις τιμές των παραστάσεων:

Ανεβάζοντας τη δύναμη ενός προϊόντος.

Για κάθε a και b και έναν αυθαίρετο φυσικό αριθμό n:

(αβ) n = a n b n

Απόδειξη:

Εξ ορισμού πτυχίου

(αβ) n =

Ομαδοποιώντας τους παράγοντες α και β χωριστά, παίρνουμε:

Η αποδεδειγμένη ιδιότητα του βαθμού του προϊόντος εκτείνεται στον βαθμό του γινομένου τριών ή περισσότερων παραγόντων.

Για παράδειγμα:

(a b c) n = a n b n c n ;

(a b c d) n = a n b n c n d n .

κανόνας: Όταν ανεβάζετε ένα προϊόν σε ισχύ, κάθε παράγοντας αυξάνεται σε αυτήν την ισχύ και το αποτέλεσμα πολλαπλασιάζεται.

1. Αύξηση σε ισχύ:

α) (α β) 4 = α 4 β 4

β) (2 x y) 3 \u003d 2 3 x 3 y 3 \u003d 8 x 3 y 3

γ) (3 α) 4 = 3 4 α 4 = 81 α 4

δ) (-5 y) 3 \u003d (-5) 3 y 3 \u003d -125 y 3

ε) (-0,2 x y) 2 \u003d (-0,2) 2 x 2 y 2 \u003d 0,04 x 2 y 2

στ) (-3 a b c) 4 = (-3) 4 a 4 b 4 c 4 = 81 a 4 b 4 c 4

2. Βρείτε την τιμή της παράστασης:

α) (2 10) 4 = 2 4 10 4 = 16 1000 = 16000

β) (3 5 20) 2 = 3 2 100 2 = 9 10000 = 90000

γ) 2 4 5 4 = (2 5) 4 = 10 4 = 10000

δ) 0,25 11 4 11 = (0,25 4) 11 = 1 11 = 1

μι)

Επιλογή 1

1. Αύξηση σε ισχύ:

β) (2 α γ) 4

ε) (-0,1 x y) 3

2. Βρείτε την τιμή της παράστασης:

β) (5 7 20) 2

Εκθεσιμότητα.

Για οποιονδήποτε αριθμό a και αυθαίρετους φυσικούς αριθμούς m και n:

(a m) n = a m n

Απόδειξη:

Εξ ορισμού πτυχίου

(a m) n =

Κανόνας: Όταν αυξάνεται η ισχύς σε μια ισχύ, η βάση παραμένει ίδια και οι εκθέτες πολλαπλασιάζονται.

1. Αύξηση σε ισχύ:

(a 3) 2 = a 6 (x 5) 4 = x 20

(y 5) 2 = y 10 (b 3) 3 = b 9

2. Απλοποιήστε τις εκφράσεις:

α) a 3 (a 2) 5 = a 3 a 10 = a 13

β) (β 3) 2 b 7 \u003d b 6 b 7 \u003d b 13

γ) (x 3) 2 (x 2) 4 \u003d x 6 x 8 \u003d x 14

δ) (y y 7) 3 = (y 8) 3 = y 24